[An updated treatment of some of this material appears in Chapter 16 of the Energy and Human Ambitions on a Finite Planet (free) textbook.]
 Now is the time on Do the Math when we scan the energy landscape for viable alternatives to fossil fuels. In this post, we’ll look at tidal power, which is virtually inexhaustible on relevant timescales, is less intermittent than solar/wind (although still variable), and uses old-hat technology to make electricity. For this exercise, we mainly care about the scale at which the alternatives can contribute, leaving practical and economic considerations sitting in the cold for a bit (spoiler alert: most are hard and expensive). Last week, we looked at solar and wind, finding that solar can satisfy our current demand without batting an eyelash, and that wind can be a serious contributor, although apparently incapable of carrying the load on its own. Thus we put solar in the “abundant” box and wind in the “useful” box. There’s an empty box labeled “waste of time.” Any guesses where I’m going to put tidal power? Don’t get upset yet.
Now is the time on Do the Math when we scan the energy landscape for viable alternatives to fossil fuels. In this post, we’ll look at tidal power, which is virtually inexhaustible on relevant timescales, is less intermittent than solar/wind (although still variable), and uses old-hat technology to make electricity. For this exercise, we mainly care about the scale at which the alternatives can contribute, leaving practical and economic considerations sitting in the cold for a bit (spoiler alert: most are hard and expensive). Last week, we looked at solar and wind, finding that solar can satisfy our current demand without batting an eyelash, and that wind can be a serious contributor, although apparently incapable of carrying the load on its own. Thus we put solar in the “abundant” box and wind in the “useful” box. There’s an empty box labeled “waste of time.” Any guesses where I’m going to put tidal power? Don’t get upset yet.
The Sphere Makes a Good Point
Tides are simply a consequence of putting an extended body in the gravitational field from another body. We exert tides on each other, in fact—though don’t try to use this as an excuse for the bulge that forms around your waist this holiday season!
Some gravity background: since Newton’s time, we have understood gravity to vary as the inverse square of the distance between masses. So gravity scales like 1/r², where r is the distance between sources. Even Einstein’s General Relativity (replaces Newtonian Gravity) respects this relationship, and we have tested that it is accurate to better than a part in ten billion using the lunar orbit. One gnarly consequence of the inverse-square law is that the gravitational force from a spherical body (planet, moon, star, etc.) is exactly the same as if all the mass were located in a point at the center of the body. In other words, the dirt under your feet plays some role in tugging you down. That dirt is very close, so 1/r² is large, but there is not much dirt right under you. Meanwhile, dirt on the other side of the Earth also exerts a pull. There’s more of it (within a given cone angle, for instance), but its pull is much weaker by the same factor. It all evens out to produce an effective gravitational pull toward the center of the Earth, as if all the mass were located there.
As an aside, if the Sun turned into a black hole—keeping its present mass in the process—Earth’s orbit would not change. The Sun is already acting like a gravitational point as far as the Earth is concerned. All that matters is mass and distance to the center, as far as gravity is concerned. Of course in this scenario, I would have to drastically revise my statements about the abundance of solar energy in last week’s post.
Tidal Origin
What does this have to do with tides? Well, the Moon—siting about 60 Earth-radii away— pulls on the Earth as if from a point. And the extended size of the Earth means that if we say the gravitational pull from the Moon at Earth’s center has strength 1/60², the pull on the near side is 1/59², while the pull at the far side is 1/61². In other words, the Moon’s pull varies by ±3.4% as we cross the Earth. Compared to the average response of the Earth (its center), the side facing the Moon really wants to get closer to the Moon, while the side opposite doesn’t understand what all the fuss is about, and is more sluggish in its attraction to the Moon. The result is an eager bulge on one side and a lethargic bulge on the other side. This is why a location sees two high tides per day, as the Earth rotates under the Moon-pointing bulge (but interaction with continental shelves/coastlines can delay it significantly, so that seeing the Moon high in the sky only means you’re at high tide in the middle of the open ocean).
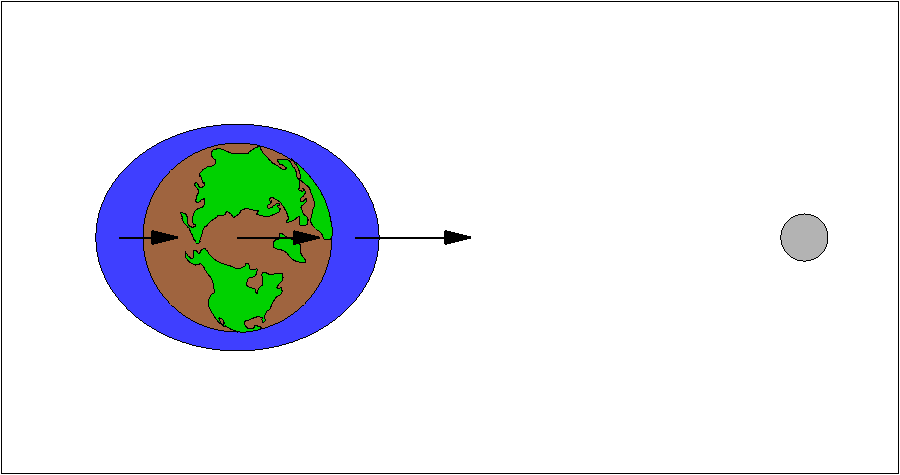
Why tides raise two bulges on Earth: one side is eager and the other reluctant compared to the average Earth response. Nothing is to scale.
Meanwhile, the Sun is 23,500 Earth-radii away, so its gravity varies by only ±0.0083% across Earth. But the Sun’s gravity on Earth is about 180 times stronger than that from the Moon, so the absolute force variation from the Sun across the Earth is about 45% as much as it is for the Moon (180×0.000083/0.034). During new and full moon, the Earth, Moon, and Sun are in a line and the bulges add (spring tides). At quarter moon, the high/low from the Sun partly fills in the low/high from the Moon, diminishing the amplitude (neap tides).
For the mathy among you, because tides deal with a difference of force across a small change in distance, tidal force is just the derivative of the underlying gravitational force times the displacement distance. Differentiating 1/r² gives 2/r³, so that the force difference is proportional to 2ΔR/r³, where ΔR is the displacement from the nominal (center) point. For numerical simplicity, I expressed everything above in units of Earth’s radius, so ΔR = 1.
Slosh Factor
For a perfect fluid body (oceanic Earth), the lunar tides would result in a peak-to-trough tidal amplitude of approximately one meter. To get the scale, we realize that the Moon’s mass is one eightieth that of Earth’s and 60 times farther away from the oceans as the Earth center. So lunar gravity is 1/(80×60²) times that of Earth gravity. Since we saw earlier that lunar tides constitute a 3.4% variation of lunar gravity, we end up with the Moon’s gravity varying by ±1.2×10−7 times Earth’s gravity. A small number, yes, but we multiply by the radius of Earth (6378 km) to get the deformation height that establishes potential energy balance. Now we have 0.75 m. Add in solar tides, and we’re close to a meter.
Most of us have seen tides well in excess of a meter. Some special places exceed 10 m, but even run-of-the-mill places like Puget Sound have 4 m tides, and San Diego gets 2–3 m. These are all exhibiting a sloshing that happens in shallow water or geographic restrictions. Take a look at tides in Hilo, Hawaii for contrast. Popping out of deep water in the middle of the Pacific Ocean, Hawaii gets open ocean tides with an amplitude of about—wait for it—a meter.
In the middle of the ocean, water does not have to move very far to raise the tide. Everyone just scrunches a little closer together laterally, forcing some water up. But introduce a continental shelf or an inlet, and we have a pinch point so that lots of water must actually flow past the bottleneck to raise a tide on the other side of the restriction. The flow can get carried away and rise up on the shore more than the tides actually demanded. The sloshing sometimes gets really out of hand when the geography produces a resonant cavity: when the natural fill/drain period is close to the six-hour tidal span. It’s just like how pushing on a playground swing at the resonant frequency produces big motion with little force (kids hate when I push because I like to experiment with out-of-phase pushes).
Putting Tides to Work
These special resonant-sloshy places are natural candidates for harnessing tidal power. Open the gates for the flow, close it off and exact a toll on the ebb. If you’re really clever, you can charge both ways. As we saw in the post on pumped storage, the power available to a hydro dam, in Watts, is P = ρFgh, where ρ = 1000 kg/m³ is the density of water, g = 10 m/s² is surface gravity, F is the flow rate of water in cubic meters per second, and h is the height of the water behind the dam.
Compared to most hydroelectric facilities, whose heights can be over 200 m, the tidal h is puny. The only other knob we have is the flow, F. And this is determined by the area impounded, the height of the tide, and the timescale over which the height difference is exploited. We have little choice over the latter, as time and tide wait for no dam.
In fact, this brings up the interesting point of choreography. We need a height difference on either side of the barrier in order to extract energy, so the inside tide and outside tide cannot be perfectly in phase with each other: this is what happens when no barrier is present. And they can’t be perfectly out of phase, since the only way the inner tide can rise is if the outer tide is bigger at that moment. It turns out, the only cases that make physical sense have the inner tide delayed by zero to one-quarter cycle—where a cycle is about 12 hours, or one high tide to the next. The maximum power extracted happens at a one-eighth cycle (45°) delay. The following (busy) chart shows the optimal sequence.
The black curve is the outside tide, going from high to low and back to high. The solid blue curve is the inner tide delayed by 1/8 cycle. Note that it reaches its max/min right when it crosses the outer tide. This must be true if the difference between outer and inner determines the direction of flow: the blue curve descends (drains) when it is higher than the black curve, and ascends (fills) when the black curve is higher. Note that the blue curve must sacrifice some amplitude (it’s not as high as black curve, or external tide). The dashed blue curve is the height difference between outer and inner tides. The red curve indicates power extraction: highest when the height difference and flow (rate of change of the solid blue curve) are at their maximum. Power goes slack when the height difference and flow momentarily stop. Note that the average power is half the peak power. For real stations peak power is experienced during the largest spring tides, so the average power across all tides will be less than half the peak capability.
The average power extracted in the ideal scenario is Pavg = (1/8)πρgAH²/T, where A is the area impounded, H is the peak-to-peak tidal amplitude, and T is the period (about 12 hours). This works if there is no bottleneck in getting water into and out of the barrier, and I have not factored in conversion efficiency (around 90% for hydro).
Compared to the naïve picture of emptying a volume, V = AH, of water with an average height of ½H in time T, the 45° phase scheme gets about three-quarters the average power of the dumb guess (Pavg = ½ρgAH²/T).
Real and Imagined Installations
The Rance tidal power plant in France, built in 1966, has a peak capacity of 240 MW, impounding 22.5 km² on an average tidal amplitude of 8 m. Because it cannot always be generating at full capacity, it effectively gets 40% of this on average, or 96 MW. The dummy model above computes 125 MW from these parameters, so not bad. The Rance station was recently surpassed as the largest tidal power plant in the world by the Sihwa facility in South Korea, edging our Rance with 254 MW of peak capacity and 30 km² of impound.
That these modest plants are the largest yet built is some indication of the limitations of tidal power. If it were easy to snatch this freebee from nature, we would see the straightforward technology implemented all over. South Korea is currently building another, larger plant expected to peak at 1.3 GW and 21% capacity factor for 2.4 TWh of annual electricity.
But some people speak of bigger plans. The large Penzhina Bay at the armpit of the Kamchatka Peninsula in Siberia (not a comment on the region or people: merely a geographic analogy) has an area of 20,000 km² and 10 m tides. Cha-ching! It is thought this could provide as much as 87 GW if fully developed. A list of proposed future concepts total about 115 GW.
Global Potential
Clearly there are special locations where tidal power can be easily trapped and put to use. In this sense, tidal is a lot like geothermal power: mostly diffuse, but with a few hotspots. By all means, grab it where it’s easy. To put things in context, the world operates today on an energy diet of 13 TW. The 115 GW of dreams mentioned above—when combined with a typical 30% capacity factor— represent 0.26% of our global demand. Hopefully, we’ve overlooked 400 times more potential than what we see in the best spots. Hmmm.
Let’s get bold with math and break free of the 115 GW shackles! How much could conceivably be harnessed? We will first escape the confines of shorelines and go for the bulk of tides: the open ocean, baby! Don’t ask me how, but let’s trap the one-meter-high bulge on each side of the globe twice daily. The surface area of Earth is πR² ≈ 5×1014 m². Trapping half the ocean means about 2×1014 m². We then have 2×1017 kg of mass raised, on average, 0.5 m for our 1 m tidal height. The potential energy, mgh is then 1018 J. Releasing this twice daily (every 45,000 seconds) constitutes 22 TW for a whole-Earth-scale project.
Sorry, am I being ridiculous? It’s not a real proposal, just a mechanism to get a handle on scale. Only slightly less ridiculous is to use the increased tidal amplitude over continental shelves and ring our continents with walls to impound and tax the ebb and flow. So let’s imagine walls 100 km out to sea where shelves exist. Not all shorelines have shelves, but imagine that such shorelines are enough to circle the globe once, or 40,000 km. For a tidal height of 2 m (average 1 m) and 4 million square kilometers, we get 8×1016 J of energy. Dumped twice a day and we get about 2 TW total. And you thought the Great Wall in China was impressive.
If you’re thinking that I should have ringed the world twice instead of once to get all applicable shorelines, then just like when a student comes to me with a complaint about the partial credit grading on an exam problem, I’ll point out that I did not exact realistic efficiencies, capacity factors, and phase choreography effects. Want me to make it worse? Still, this scheme is a completely impractical proposition.
A final measure of scale comes from my own line of research. The Moon is slipping away from us at a rate of 3.8 cm per year due to tidal dissipation on Earth. Friction as the continents rotate through the water-bulge like a super-slow egg-beater drags the bulge slightly off the Earth-Moon line, providing a gravitational “carrot” urging the Moon to accelerate forward in its orbit. The extra angular momentum imparted to the Moon (robbed from Earth as its rotation slows) causes the orbit to swell. I’ll spare you the potential/kinetic energy calculation here, but the result is a change of 4×1018 J every year, working out to 0.1 TW. So natural barriers interacting with all the tides around the globe siphon 0.1 TW from the lunar orbit. The wild schemes above would exceed this amount, which is certainly possible—i.e., the current 0.1 TW is not a top-down constraint. Extracting tidal power at the rate of 115 GW—the total of proposed projects—would double the egress rate of the Moon and further slow Earth’s rotation. Not to worry though: I’m guessing you don’t notice or care about the current rates of egress/slowing, so why would doubling either be cause for concern?
Put it in a Box
I have tidal power dangling from my fingers. I hover over the “abundant” box momentarily simply for amusement. I move over to “useful,” where we put wind power due to its practical capability of producing perhaps several TW of power and offsetting more than a sliver of our present demand. Tidal doesn’t fit here, so I’ll drop it in the “waste of time” box.
Who labeled these boxes? I want to register a complaint! Tidal is useful, in that it is practical to extract energy from nature in this way. In some select places, tidal power lights real lights, toasts real croissants, and displaces real fossil fuels. But my overall goal is to assess which forms of power can take on a substantial fraction (possibly up to a quarter) of our power needs. Only those sources capable of expansion at this scale stand any chance of achieving even half of that. Tidal is not one of those players.
To be clear, I’m not trying to discourage pursuit of any viable alternative to fossil fuels. What I do want to discourage is the sense of comfort we get because we’ve heard of lots of solutions to our energy problems (tidal, wave, geothermal, energy from trash, etc.). When we imagine a smorgasbord of options in front of us, we think we’ll never go hungry. But when the plate arrives and it’s a raisin here, a crumb of bread there, and a speck of cheese there, the variety alone is no longer a source of satisfaction. It’s happened to me in shi-shi restaurants.
As I said in the post on the meaning of sustainability, it is as unlikely that a hundred 1% solutions will satisfy us as it is that we could strap enough gerbils together to make a serviceable pony. We need a few solid, scalable, reliable solutions to fall back on. And tidal is not one of those. It’s more like a decoration than a foundation. Let’s use it where we can, but I don’t want anybody sleeping better.
Views: 2675


Totally agree on the philosophy and conclusions here. When ideas such as tidal are criticized people often defend them with “Well I don’t think there is any one single solution – rather we need a mix of generation technologies to address the energy crisis”. True, perhaps. However, as you’ve just reinforced, tidal won’t be one of them in any meaningful sense.
I really doubt whether it’s worth pursuing at large scale ANYWHERE. The environmental impact of putting an entire bay through a tidal barrage must be significant, and the fact that tidal is totally inadequate on a global scale suggests that clean/abundant alternatives MUST be developed. So why wreck the bay at all?
Perhaps a waste of time to those who care only about the result, but a most worthwhile exercise for anyone who loves physics!
Tom: While reading your recent posts I suspected that a “tides” would be coming soon to “Do The Maths.” Apropos, I recently visited the Bay of Fundy, witnessed its humongous, dramatic tides, and was pointed to the literature on the potential for making electricity with these tides. Why they don’t might be that they don’t feel comfortable with affecting tides down the coast. My host on the trip, an oceanography prof. said that the main reason is that Nova Scotia has cheap electricity as a result of Canada’s feed in tariff policies.
“The simulations suggest that up to 6.9 GW of power can be extracted (from the Bay of Fundy tides); however, as a result, the system is pushed closer to resonance which causes an increase in tidal amplitude of over 15% along the coast of Maine and Massachusetts. The tides in the Minas Basin will also experience a decrease of 30% in amplitude if the maximum power is extracted. Such large changes can have harmful environmental impacts…”
http://www.siam.org/students/siuro/vol1issue1/S01006.pdf
Fascinating—thanks!
Another great article Tom.
I am really glad there are people like you who can “do the math” as far too many people seem to fall into the trap of “technology will save us.”
I try to explain to my friends that technology can not solve all problems, but most people want, maybe even need, to believe there is a magic cure.
I think of problems like our energy future as the same as weight loss plans. Most people know that if you eat less & workout more and you will lose weight. Likewise the best solution is probably to not use so much energy, but as someone who carries a few extra pounds I can say its much easier to know the right thing that to do it.
Thanks for a fine tidal energy analysis.
No doubt I’ve missed or am forgetting an explanation provided in an earlier post of the world power ‘diet’ figure used here, 14 TW, but in the replacement context isn’t that a bit high? Total *primary* world power, all sources, is about 16.5 TW per EIA. Of that, maybe 15% is existing hydro, nuclear, biomass or wind which needs no replacement soon, if ever, leaving 14 TW of primary fossil fuel energy to be replaced with secondary energy from marine based electrical sources. Energy for heating needs to be replaced Watt for Watt, but the rest of it – transportation and all fossil electrical energy replacement gets cut in half, at least, when the Carnot cycle is eliminated in a theoretical world converted to tidal energy, thus perhaps 9-10 TW seems more appropriate for replacement. If the objection is along the lines of transportation (esp. aviation) won’t be electrified any time soon, fine, but then we agree to set transportation aside for the moment and the fossil energy to be replaced by tidal (or source X) shrinks accordingly.
Fine. Use 13, 10, 9, or anything in that ballpark. None of my arguments will ever hinge on separating those options. I’ve sometimes reduced the 3 TW used by the U.S. to 2 TW in an electric-only scenario, for much the same reason as you highlight above. But the main point is that we need replacement at the 10 TW-ish scale, and in this case, tidal will not contribute significantly to that goal.
“Energy for heating needs to be replaced Watt for Watt,”
Not necessarily! It does for simple resistor-based electric heating, but there are heat pumps, basically like air conditioning the outside, which apparently can provide 4 J heat for 1 J work. Instead of just running the electricity through a resistor, you use it to pump some heat in from outside, even against the gradient. Air-sink ones may have to fall back to resistor when it gets really cold — a decreasing problem, perhaps — ground-sink ones seem more robust.
So, US uses 3 TW; without looking it up, say that’s 1 TW heat, 1 TW electricity generation (generating 300 GW of actual electricity), and 1 TW transportation (generating maybe 200-300 GW of motive power?) Full electrification might need <300 GW for running heat pumps, 300 GW of today's power, <300GW for electrified transport (I envision light rail or trolleybuses) more than electric cars).
(Also need fuel synthesis for planes/shipping/ground vehicles that need it, I'm guessing that'd be small compared to the mass of cars. Some fuel is probably burned for high industrial heat, not the modest heat of domestic needs. Need to replace natural gas for fertilizer use. May need more desalination in the future. Etc.)
So potentially need under 1 TW for the USA, and 5 TW for the current world, if the same scaling applies, which it probably doesn't. For First World World of 9 billion people at US standard of living, you'd need 30 TW even at that efficient number.
Even at 1 TW, when compared to 22 TW as a theoretical maximum for extracting all tidal energy from the entire ocean, and 2 TW for great continental walls, tidal doesn't look globally relevant.
Hi Tom
Here in the UK there have been regular investigations on tidal schemes for the River Severn / Bristol Channel, which, due to natural funnelling, has a very wide tidal range. 30 billion pounds was the last proposal, to generate 5% of current UK electricity demand. Not necessarily when we need it, as the tides don’t coincide with the electrical demand peaks, though that’s still a better bet than intermittent wind or solar, in a UK context. Still, if it was tidal lagoons rather than barrages, that might allow for better river flow and reduce the environmental impact, and allow pumped storage and/or timed release at peak demand. It would last a hundred years or more and provide at least some energy for future generations, but it seems we don’t care too much for those guys. Thirty billion quid would be the come-on price, mind – bound to increase once we got the builders in. Pretty much academic though, as we just burned our way through the North Sea Oil and spent the proceeds, and then some. Perhaps we could print the cash.
Just a note to would-be contributors. I’ll be addressing other energy ideas over the coming months, but one at a time, and in no particular order. Please be patient and hold off on comments to the effect: “we should be pursuing X, because it’s far more capable than tides.” We’ll probably get to it. For now, any thoughts on tides or the role they might play or how we should react to bit-players in the energy game?
You know, one comparison that would be nice would be with solar, the (current) reigning champion.
How big a PV array would you need to equal the theoretical maximum output of tidal (and wind), and how big an array would you need to equal the current largest in-production facility? “Facility x cost $y and generates z MW. For $n at today’s going rate, you could build a PV array the same size and it would take q as much real estate.” That sort of thing.
I think something along those lines would help put things in perspective. If nothing else, it would help clarify if something like tidal that goes in the “don’t bother” long-term bucket might still make sense in the short term — that is, whether or not it’s worth considering in the interim while we (I hope) ramp up to solar.
Cheers,
b&
Contender: Incheon Tidal
GW: 1.3
Capacity Factor: 21%
Annual Energy (TWh): 2.4
Cost : $3,400,000,000
Area: Dunno, 44 *BIG* turbines.
Solar: Average site (15% cap factor)
GW: 1.82
Capacity Factor: 15%
Annual Energy (TWh): 2.4
$/kW: 4000
$ Total: $7,300,000,000
Land fill factor: 80%
Nominal Insolation (kw/m2): 1
Efficiency (%): 18%
Area (m2): 84,000,000 (1/2 of the tidal basin at Rance, which is 1/5th the size of Incheon)
—–
I matched for energy, not power. The above suggests that the Incheon plant would cost around half as much as today’s utility scale solar benchmark for installed cost.
Of course, that value will probably be cut in half again (hoepfully more) over the next ten years. And I wouldn’t be at all surprised if the installed cost of the Incheon project doubles.
In fairness though, for something like Rance the bulk of the cost is in the barrage, which will last a really long time. Wikipedia says the generation cost there is now well below nuclear.
Still, has a significant environmental impact and not a big enough energy impact to be worth the bother really. I think we need to focus on things that will work on a meaningful scale, not national prestige projects that soak up a lot of money while creating no worthwhile technology springboards.
One disadvantage is the solar option inevitably requires more backup or storage than tidal, unrelated to capacity factor which is an averaged figure. Using the assumptions of the Storage post, solar and tidal both need short term but predictable back up on the order of hours, but solar alone needs additional if less frequent backup for 2-7 days.
Hardly matters if tidal is forever a tiny contributor. Yes, storage is much simpler. I wish tidal were the answer.
Just an update to my numbers here for the closing of 2011 – there are now several credible reports of large scale solar PV plants with installed cost in the $2/watt range. Which means that solar PV, even on a average-to-poor site, already delivers energy at a lower cost than highly speculative tidal projects that will never make a large scale difference anyway.
The case, it be closed.
“… there are heat pumps, …”
Yes of course, thanks, pumping heat vs making it escaped me in my haste.
“… For First World World of 9 billion people at US standard of living, you’d need …”
I think in projecting the first world population trend forward several decades out one should do the same with the first world energy use per capita trend, which is falling, apparently poking a stick in Jevon’s eye [1]. It’s not falling enough, but you don’t end up with 30 TW. China and India are skipping over the inefficient energy tech of the first world’s 1970s (10% vs 30% eff gas cars, 20% vs 60% eff power plants, 30% vs 60% eff jet engines, thousands of miles of copper telephone cable vs glass or 3G/4G wireless, 10 bushels per acre vs 100), thanks in part to first world technology.
[1] http://www.google.com/publicdata/explore?ds=d5bncppjof8f9_&ctype=l&met_y=ny_gnp_atls_cd#ctype=l&strail=false&bcs=d&nselm=h&met_y=eg_use_pcap_kg_oe&scale_y=lin&ind_y=false&rdim=country&idim=country:USA&ifdim=country&hl=en&dl=en
Cool. OTOH, if you give 9 billion people the US energy use today, that’s 90 TW. 30 is the perhaps optimistically electrified version. And the US actually uses less energy than Canada or Norway per capita, IIRC (not counting embodied energy in imports); part of the US’s “waste” may be cars and cheap energy, but part of it is probably a nastier ciimate relative to most of Europe. Much of the US calls for winter heating *and* summer A/C… A lot of the world doesn’t need winter heating at all, but might really like year-round A/C.
Even 15 TW — the 30 divided by another 2, and about what the world uses not so wel right now — is obviously too much for tidal.
For analysis I’d like to see hot dry rock. I think it’s not renewable but has large enough fossil reserves to be interesting, but extraction robustness isn’t tested and there’s the earthquake problem. (Or opportunity!)
Great article. I’d like to see the same calculation done with ocean wave energy. It seems to me that the energy density on a breaking ocean wave is a lot higher than the tide. I go to the beach in the summer holidays, and tried this experiment:
1 – lay in the sun. It takes many hours before I feel warm, and the sun doesn’t move my inflated beach ball.
2 – walk in the wind. It takes just a few minutes to realise that I’m exerting a lot of energy to walk against it, and the wind blows my ball away down the beach.
3 – get dumped by a crashing wave. The wave moves my beach ball and moves ME just as easily, emitting a roar of noise as a bonus to dissappate excess energy.
Conclusion – ocean waves seem much more energy dense than wind or solar, and there’s an awful lot of coastline as you point out.
I’ll be getting to ocean waves, but I’ll take an approach different than your experiment. It’s tough to compare kinetics to thermal, and in any case energy density doesn’t amount to much if the area is small. While the linear length of wave-torn beaches might be impressive, the height is not, so the effective area is very limited.
Instead of using dams and barages, why not use the “run of river” concepts. In effect, put underwater turbines in the zones where the water velocity is dent, like most of the Bay of Fundy, though preferably in the shallow spots with no ship traffic for starts. Another great candidate for these is Long Island Sound, where the estimated capacity of tidal turbines with no dam is over 2GW on an average delived basis.
The “underrwater wind turbines” just using water velocities of greater than 2m/sec are very fish friendly and would have a minimal environmental impact -those todal barages can do a lot of change, and not necessarily for the best, either. And so what if it is a bit more capital intensive -more jobs get created, too.
DB
Tidal energy isn’t quite as weak as you make it out to be here. Comparing Tidal Power to the total world power use is the wrong comparison. Much of our power (roughly half I think) gets used from 9 to 5 in the middle of the day when everyone is at work. Conveniently for us, that’s also when solar energy is abundant, as you calculated in your previous post. All we really need from tidal and wind is to help carry the load at night, when the power requirements should be much less. (although admittedly, those will increase if everyone buys an electric car that needs to be charged at night.)
Maybe you could “Do the math” on what kind of investment in wind, tidal, and solar thermal would be necessary to meet our off-peak power requirements. We can also (hopefully) improve out power grid, so that it wouldn’t matter as much if one particular area was stuck with cloudy weather.
This is only one form of harvesting tidal power, more modern forms use the underwater turbines described by Bradley above. Can you do some calculations based on those? From my limited knowledge, they seem capable of producing much more power if we can figure out how to make turbines that are safe for marine life, non-biofouling and that will not get crushed by tidal forces. I know there has been considerable work done one this.
Who cares how much of world demand a particular type of generation can meet. The important thing is to match the type to the particular environment. Here in southeast Alaska tidal has great potential and solar is pretty much worthless. The converse is true in Arizona. There’s no need to chose just one to replace fossil fuels.
I appreciate that different techniques work in different places. I’m not saying don’t do tidal. I’m all for doing it where it makes sense. And I’m not saying we need one thing to replace all of fossil fuels. What I am trying to do is sort out real players from niche solutions. Tidal is a niche. It may work in a few places for small populations, but that does not imply we don’t face a huge problem and that tidal won’t do much to solve it. So I care how much demand each type of generation can satisfy.
I think its also important to note that research dollars and engineering talent have limited resources.
I would much rather focus those resources on technologies that have the potential for global energy generation.
Tom,
I think you have riled people up by describing your third bucket as ‘waste of time’, regardless of your explanation. Perhaps labelling it ‘niche’ might help.
Very good! I agree completely on Tidal Energy being a «niche» source of energy rather than consigning it to the waste bucket/basket.
But I would not abandon the concept of «waste» − we will always need a waste basket!