After inaugurating the Do the Math blog with two posts on the limits to physical and economic growth, I thought it was high time that I read the classic book The Limits to Growth describing the 1972 world computer model by MIT researchers Meadows, Meadows, Randers, and Behrens. I am deeply impressed by the work, and I am compelled to share the most salient features in this post.
To borrow a word from a comment on the Do the Math site, I’m gobsmacked by how prescient some of the statements and reflections in the book are. Leaving aside remarkably good agreement in the anticipated world population and CO2 levels thirty years out (can’t fake this), I am amazed that many of the thoughts and conclusions I have formed over the past several years are not at all new, but were in black-and-white shortly after I was born.
Cornucopian Contrast
This post will provide many extended quotes from The Limits to Growth, the first of which are themselves quotes within the book, appearing on page 130 (all page references are based on the second edition, printed in 1974). I include these external quotes to contrast the so-far-so-good track record of The Limits to Growth in terms of providing a credible framework for how things unfold.
The first is from the 1969 book Principles of Demography by Donald Bogue—apparently still high from the Green Revolution:
Given the present capacity of the earth for food production, and the potential for additional food production if modern technology were more fully employed, the human race has clearly within its grasp the capacity to chase hunger from the earth—within a matter of a decade or two.
At present—four decades on—food production per capita is essentially stalled or declining, and each year the world has less arable land per person due to population growth compounded with soil erosion, salinity increase, desertification, and development.
Next, we have R. Buckminster Fuller saying in 1967:
Humanity’s mastery of vast, inanimate, inexhaustible energy sources and the accelerated doing more with less of sea, air, and space technology has proven Malthus to be wrong. Comprehensive physical and economic success for humanity may now be accomplished in one-fourth of a century.
I’m just pointing out to those who discount the credibility of rocky-future warnings based on repeated “failures” of such warnings to materialize, that there is perhaps a greater preponderance of hallucinatory hubris that also fails to materialize. We should approach projections of the future with humility. We should realize that there really is something special about these past few centuries (the one-time fossil fuel joy-ride), and admit that we don’t have a consensus model for what happens next. Only then can we be smart in our preparation for the unknown.
The Model Outcomes
Back to The Limits to Growth and the sobering analysis within.
The World3 model created by the research team tracked five main quantities, building in all of the apparent linkages and feedback loops that can influence their values. They were:
- population;
- industrial output per capita;
- food production per capita;
- resources;
- and pollution.
Many auxiliary variables were tracked in the process, and the graphs show birth rate, death rate, and services per capita in addition to the five main variables.
Various runs under differing assumptions about the future were used to crudely map out the dynamical modes of the complex world system. The authors are very clear that their models do not constitute predictions, but rather useful qualitative descriptions much like one might describe the approximate behavior of a ball thrown into the air (or a train crash?).
Almost independent of the scenario, the models tended to result in a declining standard of living by the end of this century—the “standard run” crashing as soon as 2020. This generic result was robust even when doubling the amount of assumed resources, aggressively recycling materials, aggressively controlling pollution, substantially increasing agricultural productivity per unit area, and implementing “perfect” birth control (no unplanned/unwanted children). All of these acting together still failed to stave off a downturn. Only by imposing strict policy changes to force zero population growth and zero growth in industrial output could they produce a stable outcome. Over the decades, increased data and model sophistication have not changed the basic modal behaviors exhibited by World3. Moreover, a comparison of three decades of data against the standard run model from 1972 shows impressive fidelity thus far.
Might As Well Be Peanut Butter
Those unfamiliar with computer modeling might easily dismiss this result. A neighbor, learning that I am an astrophysicist, once grumbled to me that he just read about astrophysicists who had used a computer model to “prove” that neutron stars were made of matter in a state similar to that inside an atomic nucleus. “Heck, I could program my computer to tell me that these stars are made of peanut butter, and that’s exactly what it would do,” he boasted. I didn’t bite: good fences make good neighbors.
Those who understand that such models involve defining the fundamental interactions and requiring self-consistency at every step in the evolution would not discount the genuine value of a computer model out of hand. In my neighbor’s case, the peanut butter star—if fully modeled by all the relevant physics we know—would find itself unable to support its own weight against gravity, would collapse, the intense overburden ultimately overwhelming the degeneracy pressure exerted by electrons, forcing the electrons and protons to join into neutrons. Presto mundo: peanut butter star becomes neutron star.
But those in the know are also aware of the “garbage in, garbage out” pitfall: that unrealistic initial conditions and/or model dynamics can render the output meaningless. While I can’t personally vouch for the viability of the World3 model—it does, after all, have to cut corners in modeling something as complex as global human activity—I can offer my take based on my limited exposure.
Model Insights
First, although not the most important aspect, the researchers earned my respect in describing their approach and attitudes. They come across as honest scientists trying to do the best, most realistic job they could in getting the story right. They were careful to explain assumptions, disclose the limitations of their approach, and gave the model every chance to find Utopia. I got the impression that they were shocked and dismayed by the stark and universal outcome of their scenarios.
But mostly, the model supported the common-sense notion that combining a growth paradigm with finite resources and a delay mechanism, overshoot is an expected response. After overshoot comes a decline.
Here is my description of how and why this works. Growth is a positive-feedback, or self-reinforcing mechanism: more people result in more reproduction; more industrial capital means more manufacturing; more money means more to invest in fueling additional growth. Negative feedback is self-correcting: overgrazing means less food available, exerting downward (corrective) action on population; machines wear out, diminishing the ability to make more machines; the effects of pollution lead to ills that drive measures to decrease pollution. If the negative-feedback mechanisms are delayed in relation to the positive-feedback mechanisms, overshoot occurs so that the correction will be more substantial when it arrives.
For example, decisions to have children are based on conditions now rather than on the state of the world 30 years later when that person still needs to be fed and is reproducing. Pollution is emitted now in relation to today’s growing industry, although its deleterious impacts may not be realized for decades. The self correction of starvation or poor health may not “inform” the positive-feedback mechanisms until they have had ample time to drive the system far past its limit.
A particularly apt analogy from the book paints this picture nicely (p. 144):
Delays in a dynamic system have serious effects only if the system itself is undergoing rapid change. Perhaps a simple example will clarify that statement. When you drive a car there is a very short, unavoidable delay between your perception of the road in front of you and your reaction to it. There is a longer delay between your action on the accelerator or brakes and the car’s response to that action. You have learned to deal with those delays. You know that, because of the delays, it is unsafe to drive too fast. If you do, you will certainly experience the overshoot and collapse mode, sooner or later. If you were blindfolded and had to drive on the instructions of a front-seat passenger, the delay between perception and action would be considerably lengthened. The only safe way to handle the extended delay would be to slow down. If you tried to drive your normal speed, or if you tried to accelerate continuously (as in exponential growth), the result would be disastrous.
A Simple Delay/Overshoot Model
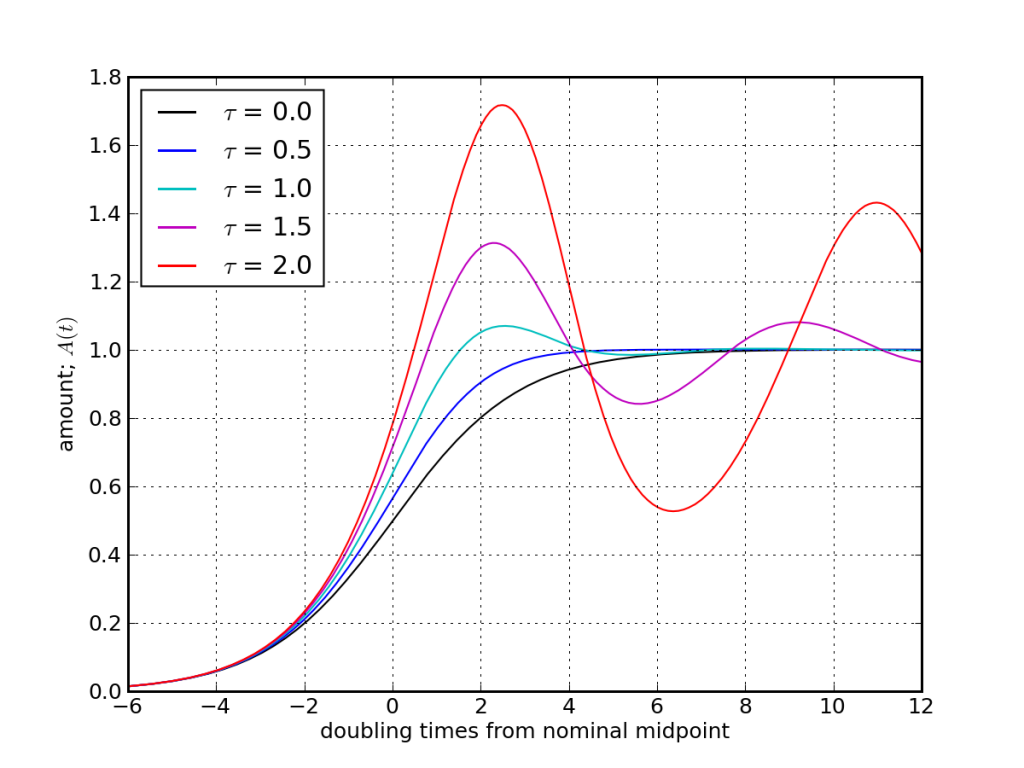
I had to see this for myself in a simple model. So I inserted a delay mechanism into the negative feedback portion of the differential equation describing the logistic curve. This is the standard S-shaped curve followed, for instance, by a population adapting to a fixed rate of nutrient input. We often think of the logistic curve in terms of population, but it could also represent standard of living, energy production, agricultural output, or other quantities that we might think (or hope) will stabilize at some equilibrium value in the future. In general, we will denote the amount (of whatever) at time, t as A(t).
When no delays are present, the rate of growth is proportional to the amount (e.g., population) currently in place times the “open resource” still available. For instance, if the amount is scaled so that it levels out at a value of A(∞) = 1.0, the logistic rate equals A(t)×(1 − A(t)). The solution to this relation is that the amount follows A(t) = 1/(1 + e−t), where ex is the exponential function. It starts out at 0.0 at large negative times, is at ½ at t = 0, and approaches 1.0 at large positive times.
Early on, the “available” space is 1.0 (virtually all of it unoccupied), and the rate of growth is just proportional to the amount—which is the condition for exponential growth. This is the positive feedback part. The (1 − A(t)) piece is the corrective action that over time acts to reduce the rate toward zero, and is thus the negative feedback piece.
Inserting a delay means that the amount (e.g., population) today is responding to the negative feedbacks (brought on by the available space/resource) of yesterday. So we express the rate as A(t)×(1 − A(t − τ)), where τ is the amount of delay.
The figure above shows the result of adding various delays, τ. The black curve is the straight-up logistic curve with zero delay. The time axis is scaled to doubling times at the initial exponential rate (for a constant growth rate of x%, the doubling time is 70/x years). As we add more delay, the curves begin to overshoot by larger fractions, and ultimately oscillate toward the eventual value of unity.
Let’s be clear that I do not claim this to be a model of our future! It’s a simple demonstration of the generic effect delays have in what would otherwise be logistic behavior. There are all kinds of reasons behavior may not be logistic. If a population explosion of rabbits overgrazes the available land, erosion may result, removing topsoil vital to the support of growing back the resource. The act of overshoot can therefore reduce the ultimately sustainable value (in contrast, the model above converges to 1.0 in all cases). Likewise, overtaxing agricultural lands results in soil loss, increased salinity, and/or desertification, reducing the overall carrying capacity of the land. Also, who is to say that we can achieve level energy usage? A failure to implement replacements for fossil fuels at a grand scale could deny us an energy operating point as high as we enjoy today.
Faith in Technology
Many of us are technological optimists, and have faith that we will cleverly craft our way out of a bad situation when the need drives us—as we have often done in the past. But to the extent that we need social changes—like a steady state economy, truly sustainable attitudes, or a paradigm shift from a generations-old mentality centered on growth—we may find it difficult to adapt in time. The Limits to Growth authors say (p. 148):
While technology can change rapidly, political and social institutions generally change very slowly. Furthermore, they almost never change in anticipation of a social need, but only in response to one.
Most delays, physical or social, reduce the stability of the world system and increase the likelihood of the overshoot mode.
The authors wrap up the thought after describing the crisis conditions confronting the whaling industry in the early 1970’s (p. 151):
The basic choice that faces the whaling industry is the same one that faces any society trying to overcome a natural limit with a new new technology. Is it better to try to live within that limit by accepting a self-imposed restriction on growth? Or is it preferable to go on growing until some other natural limit arises, in the hope that at that time another technological leap will allow growth to continue still longer? For the last several hundred years human society has followed the second course so consistently and successfully that the first choice has been all but forgotten.
There may be much disagreement with the statement that population and capital growth must stop soon. But virtually no one will argue that material growth on this planet can go on forever. At this point in man’s history, the choice posed above is still available in almost every sphere of human activity. Man can still choose his limits and stop when he pleases by weakening some of the strong pressures that cause capital and population growth, or by instituting counterpressures, or both. Such counterpressures will probably not be entirely pleasant. They will certainly involve profound changes in the social and economic structures that have been deeply impressed into human culture by centuries of growth. The alternative is to wait until the price of technology becomes more than society can pay, or until the side-effects of technology suppress growth themselves, or until problems arise that have no technical solutions. At any of those points the choice of limits will be gone. Growth will be stopped by pressures that are not of human choosing, and that, as the world model suggests, may be very much worse than those which society might choose for itself.
They immediately wrap up the thought with a shout-out to the technology optimists among us:
We have felt it necessary to dwell so long on an analysis of technology here because we have found that technological optimism is the most common and the most dangerous reaction to our findings from the world model. Technology can relieve the symptoms of a problem without affecting the underlying causes. Faith in technology as the ultimate solution to all problems can thus divert our attention from the most fundamental problem—the problem of growth in a finite system—and prevent us from taking effective action to solve it.
Exactly. It is not wrong to dream of a happy technological end-state, or to wish for a convenient pill for any ailment. How could we possibly arrive in such a state without first conceptualizing the dream? But if our faith is so strong that we assume that’s where we are heading, based on extrapolation of our fossil-fueled joy-ride, then we don’t go all-out to avoid the real danger of a crash. Like the nerd in the school cafeteria, our mental state is so consumed by mathy/techno thoughts that we fail to notice the stupid stuff like the stool in our path (hitting a little close to home here).
The very fact that most people (I think) consider a crash to be unlikely is in some ways the most scary aspect of the story: our guard is down. Only by taking the crash scenario seriously can we take concrete actions to avoid it. I can concoct loads of worst-case scenarios that are freakishly unlikely to transpire, but the unglamorous tale of pushing growth against finite resources and failing to let go of fossil fuels before they drag us down actually has some teeth. It’s what the impassionate World3 model portended. Wisdom suggests not dismissing the result.
Postscript: Coincidentally, another blog post by Ugo Bardi on The Limits to Growth appeared at almost the same time as this post. It has some nice illustrations of the model and its results complement this post nicely.
Views: 7386
Do You think this overshoot and decline could be overcome? Is it unavoidable or could some – realistic – measures at some (national? global?) level help? What would they be?
Also, I’d love to thank You for this insightful blog 🙂
[shortened by moderator]
Fantastic post. I’m convinced that the way to get this into the mainstream is to convince the economists though. However, mainstream economists will never be convinced with a model that ignores prices and incentives, and which uses fixed factor “rules of thumb” for how resources interact with capital and labour to create economic activity, and how economic activity then determines capital stock.
We need a LTG style model that includes prices and incentives to engage with the economics profession. We need to work together.
I’m trying (as part of an economcs PhD) to show that including prices and incentives in a LTG type model is not sufficient to avoid collapse – indeed even in a model without ultimate limits, prices and incentives can cause a collapse as the quality of the resources becomes poorer.
If you have an industrial economy exploiting ever more marginal energy resources, which require ever more capital intensive extraction. It relies on economies of scale in the manufacturing sector (which is a reasonable assumption). As the energy supply is constrained, the scale of this sector declines, leading to sudden collapse.
See http://dcomerf.pbworks.com/w/file/44827982/An%20Industrial%20Economy's%20Response%20To%20Declining%20Energy%20Resources%20(presentation).pdf if you’re interested.
Interesting to see the effect of delays in logistics curves. In feedback control systems delays are *always* destabilizing (see Franklin, Powell & Emami-Naeini, Feedback Control of Dynamic Systems, 6th Ed., pp272-274 and pp381-382 for demonstration using Root-Locus and Bode plotting techniques). This applies to high-order systems as well as the low-order approximation given by the logistics curve (which a controls engineer would call a first order system).
[shortened by moderator]
Your readers might like to know about Ugo Bardi’s work. Ugo is a professor of chemistry at the University of Florence with a long-standing interest in system dynamics and Limits to Growth (LtG). Ugo has recently published a book called Limits to Growth Revisited in which he discusses the reactions to the original LtG.
Naturally Ugo also has a blog. In his most recent post he discusses the reaction to LtG: “Critics had to work hard to find weak points in the study that went beyond simple statements of disbelief . . . In the end, they had to settle on very minor points that had no relevance to the significance of the study.”
That incredulity is the problem. The LtG study isn’t “mind-sized”: the model is not immediately graspable, and this psychological difficulty causes people to reject it.
That post is here, and Ugo’s post about his book, with a link to its introduction on Google Books, is here.(Disclosure: I have no connection with Ugo other than reading his blog, and intending to buy his book.)
But fairly simple assumptions lead you to similar conclusions to LtG?
1) We live in a closed system
2) Thus there are finite resources
3) Growth in resource usage is exponential, human thought models things linearly.
4) There are delays in feedback,
5) Thus there is a lag in between our perception and the current resource usage.
6) This lag is the source of the instability.
The logistic curve + delay above shows how easy it is to get to an unstable state.
The thing that makes our current growth an existential threat is the fraction of planetary resources that are being controlled by humans at this point. There aren’t really spare resources to provide a cushion to a shock.
I think we must note that people like to talk and theorize much more that to actually do anything and therefore we can be certain we will have many discussions, solutions, scenarios played out, books written, blogs typed before an eventual crisis. It is from this rich pool of ideas we could perhaps draw a real solution. This is the important part science fiction, academia and theoretical ramblings play in protecting humanity. Out of impracticality, laziness and dreaminess, salvation is born.
The most important lesson (maybe) from LTG: If any element of a dynamic system is unsustainable, then the system is unsustainable.
Second most important lesson (also a maybe): Innovations make long term forecasting a bit challenging.
“Like the nerd in the school cafeteria, our mental state is so consumed by mathy/techno thoughts that we fail to notice the stupid stuff like the stool in our path (hitting a little close to home here).”
This, ironically, reads like an apt description of the Limits to Growth authors (as well as this blog). There seems to be a real belief that just “doing the math” will let you actually predict the future, including the far future, despite great numbers of repeated, highly public, and highly embarrassing failures (stools in the path, so to speak). This unshakable faith appears to be predicated upon the simple and obvious notion of a “finite system”, even though, as far as we know, space is not finite. It’s true, of course, that the further out in space and time we push, the more “fantastical” the scenarios of further growth appear to us, but that’s merely a limit inherent in our imaginations, and no more real than the faith-hobbled imaginations of people 1000 years ago, for whom our present would no doubt appear fantastical.
I’d rather not have a showdown between dreams and physics/math, because both are useful to us. But if forced to bet on one, I’ll pick physics. I heard an undergraduate student recently say: “If it can be imagined, it can be done,” getting nods from other students. It takes my imagination less than two seconds to violate this axiom. Dreams are great, but let’s not get carried away, and ignore solving real here-and-now problems by leapfrogging our imaginations to a distant future where today’s rules don’t apply.
Science always wins over the dreams becasue there are practical limits to the natural world that dont exist in one’s dreams.
i.e. Larry
“This unshakable faith appears to be predicated upon the simple and obvious notion of a “finite system”, even though, as far as we know, space is not finite.”
even if we have an infinite system with which to expand into there is a finite speed with which we can advance. There are practical limitations just by human nature, even if we had unlimited resources with which to tap into it takes TIME to reach them. just as u cant build a house instantly u cant have sustained rate of percentile growth. The whole reason i like this blog is that it points out our limits and shows more what a reasonable expectation is given our current state of being.
But I wasn’t the one referring to “dreams”, I was simply pointing out that arguments that pertain to finite systems don’t pertain to non-finite ones. In such systems, rates of advance can certainly be finite and still allow for indefinite growth.
It’s true that I injected the word “dreams” into the argument. But that’s how I view talk of expanding into infinite space when relating to our more immediate growth limits in the next century or two. If you already know the future is unimaginably unconstrained by finite limits, then this blog is not a good use of your time, since it focuses on the actual challenges in front of our faces. And to prevent launching a fruitless argument over a future that no one can support with data, I’ll end the thread here.
I have read Graham Turners review of LtG and also the 30 year update on LtG by the original authors. I haven’t read Ugo Bardi yet, but is there any sign of the original critics “recanting” – probably not, the damage was done, and is still being done. The one thing I found hard to accept in the 30 year LtG update was the “success story” which the authors hold out as their “beacon of optimism” i.e. the Montreal Protocol banning ozone depleting chemicals. I find it hard to accept, that these success’ can be described as such. It took 24 years until the protocol was signed in ’99 and “the ban” was not imposed until just 12 months ago in a global sense. In fact it is “probably” the case that because of the lack of internal regulation within such countries as China that ozone depleting chemicals are still being used. These impacts I understand will not see the ozone layer start to be repaired until 2050 “IF” the ban is effective.
“Only by taking the crash scenario seriously can we take concrete actions to avoid it.”
Whilst I appreciate the optimistic finale to your article, it does not appear to be borne out by facts. Assoc Prof Tim Garrett published a piece earlier this year called the “Themodynamics of Civilization Growth” in which he stated that there is no way out of the mess we’re in, clearly stating that the future holds an economic and/or environmental collapse.
Looking at the U.N. C.S.D. “World Economic and Social Strategy 2011” Ban Ki Moon “mentions” LtG in passing, stating that the limits to growth theory is not new and concludes ;
“While capping the use of energy and other resources by setting limits to growth in developed countries might have worldwide benefits, to many the prospect of “prosperity without growth” may not be very appealing. One reason for the difficulty involved entails what Jackson (2010) refers to as the “dilemma of growth”—the fact that while the current pattern of growth is unsustainable, the current structure of the economy and of society is such that an economy without growth is unstable. Acceptance and implementation of prosperity without growth will therefore require major structural transformations of economies and societies.”
And that is ALL he states. What I am trying to ascertain is just exactly what “concrete actions” are available to avoid the crash that is coming ?
Thanks for the thoughtful comments. As a physicist, I cannot rule out a sustainable existence. Our future is not, in fact, pre-determined, even if our current trajectory leads to a crash. It is within our power to scale back our resource throughput by a very large factor and still live satisfied lives. We have well-thought models for a steady-state economy. The likelihood of our voluntary adoption of these measures may be utterly remote in the current climate. But there do exist concrete measures that could change the game entirely. Only if we collectively acknowledge ahead of time the grim fate of not doing these things will such concrete actions be taken. I could give up in the face of tall odds. But I’ll do what I can to raise awareness.
Glad you mentioned the Steady State, I’ve been involved with Rob Dietz for some years (although “virtually”). I sometimes think that we are being “lead by the nose” on this total inability to restructure rational economics, seems like “they” want to get as much out of the planet as “they” can (Keystone) before we are forced into a Steady State.
Acceptance of collapse is a big thing to come to terms with, and I guess I’ve done that, and like you am now just doing what I can. Thanks for your articles.
Tom: I’m interested in your basis for saying, “At present—four decades on—food production per capita is essentially stalled or declining.”
Regards, Don
I looked at many graphs from a variety of sources, and got mixed results. Grain per capita often went down, while total calories was still climbing (but more slowly than in decades past). If you have global data you feel is conclusive on the issue, I’d very much like to see it.
Tom: We might be on the cusp of a change with global food production. For the long term view, a good place for data is the FAO stats ( http://faostat.fao.org/site/609/DesktopDefault.aspx?PageID=609#ancor), but you will see the same 50 year patterns with World Bank data and USDA data. Per capita, global food production is rising, level, or falling (depending upon the commodity). But the denominator, population accounts for most of the action. Total global production of most crops continues to rise, but not as fast in the recent 5 years as in previous decades. Regionally, the stats are all over the place. For example, rice in the Philippines is a mess; they have to import increasing amounts each year. The Philippines story is most in the denominator, increasing population. However, their politics of food is pretty bad. Lots of corruption and closed markets; they could grow more food with decent policies. At the same time, rice in Thailand is pretty rosy, total production as well as per capita (not to suggest that population isn’t an issue in Thailand. China is a world to itself and is pretty proud that per capita production of major commodities is keeping up with population (the rate is falling in China). And of course weather shocks, such as those to Russia and Pakistan last year, put a lot of wobble in the lines for recent years. As well, with the huge glob of Chinese money in world markets, speculation on food has affected production in recent years; interesting topic tht involves weather and investment decisions—lots know about this. Global warming is starting to be felt, however. The best take on this angle of which I am aware is “Climate Trends and Global Crop Production Since 1980
David B. Lobell,1* Wolfram Schlenker,2,3 Justin Costa-Roberts1 Science, May 5 2011”
I would like to hear your take on the data. Regards, Don
Hey, nice antialiased curves! What graphing tool do you use? I know… slightly OT 😎
Yes: off topic, but short—and nerdy enough to appeal… I use Python for coding, the matplotlib module for plotting, producing PNG output.
Have you read David MacKay’s “Sustainable Energy Without the Hot Air”?
http://www.withouthotair.com/
I would be interested in your reactions to it.
Indeed, I am very familiar with the book, and fond of its approach. It’s even on the DtM blogroll! MacKay, like me, absorbed an order-of-magnitude approach to physics in his time at Caltech. The best course I ever took was called order-of-magnitude physics and taught by Peter Goldreich and Sterl Phinney. MacKay didn’t actually take this course, but became familiar with its content all the same.