 We’ve all heard it. We think we understand it: entropy is a measure of disorder. Combined with the Second Law of Thermodynamics—that the total entropy of a closed system may never decrease—it seems we have a profound statement that the Universe is destined to become less ordered.
We’ve all heard it. We think we understand it: entropy is a measure of disorder. Combined with the Second Law of Thermodynamics—that the total entropy of a closed system may never decrease—it seems we have a profound statement that the Universe is destined to become less ordered.
The consequences are unsettling. Sure, the application of energy can reverse entropy locally, but if our society enters an energy-scarce regime, how can we maintain order? It makes intuitive sense: an energy-neglected infrastructure will rust and crumble. And the Second Law stands as a sentinel, unsympathetic to deniers of this fact.
A narrative has developed around this theme that we take in low entropy energy and emit a high entropy wake of waste. That life displays marvelous order—permitted by continuous feeding of this low entropy energy—while death and decay represent higher entropy end states. That we extract low entropy concentrations of materials (ores) from the ground, then disperse the contents around the world in a higher entropy arrangement. The Second Law warns that there is no going back: at least not without substantial infusion of energy.
But wait just a minute! The preceding paragraph is mostly wrong! An unfortunate conflation of the concepts of entropy and disorder has resulted in widespread misunderstanding of what thermodynamic entropy actually means. And if you want to invoke the gravitas of the Second Law of Thermodynamics, you’d better make darned sure you’re talking about thermodynamic entropy—whose connection to order is not as strong as you might be led to believe. Entropy can be quantified, in Joules per Kelvin. Let’s build from there.
The Measure of Entropy
From a thermodynamic standpoint, the total entropy of a system has a simple definition. If I add an amount of energy ΔE (measured in Joules, say), to a system at temperature T (measured on an absolute scale, like Kelvin), the entropy changes according to ΔS = ΔE/T. The units are Joules per Kelvin.
This is very closely related to the heat capacity of a system or object. If we measure for a substance how much the temperature changes when we add a bit of energy, the ratio is the heat capacity. Divide by the object’s mass and we have a property of the material: the specific heat capacity. For example, the specific heat capacity of water is cp ≈ 4184 J/kg/K. If we heat one liter (1 kg) of water by 10°C (same as a change by 10 K), it takes 41,840 J of energy. Most everyday substances (air, wood, rock, plastic) have specific heat capacities around 1000 J/kg/K. Metals have lower specific heat capacities, typically in the few-hundred J/kg/K range.
So if we know the specific heat capacity as a function of temperature, and start the material out at absolute zero temperature, adding energy until it comes up to the temperature of interest (room temperature, in many cases), we can compute the total entropy by adding (integrating) all the little pieces ΔS = ΔE/T, where ΔE = cpmΔT, and m is the mass of the object of interest.
Most materials have a specific heat capacity dropping to zero at zero temperature, and rising to some nearly constant value at intermediate temperatures. The result of the integration for total entropy (sparing details) pencils out to approximately equal the heat capacity, cpm, within a factor of a few. For a kilogram of ordinary matter, the total entropy therefore falls into the ballpark of 1000 J/K.
Because entropy and heat capacity are so intimately related, we can instantly order entropies of everyday substances: metals are lowest, followed by stuff like wood and rock, and liquids have the highest (water, especially), on a per-kilogram basis.
Where is the Disorder?
Note that we have managed to quantify entropy—at least in broad brush, order-of-magnitude style—without making reference to order.
Well, it turns out that if one can count the number of quantum mechanical states available to a system at a given (fixed) energy—in other words, counting all the possible configurations that result in the same total energy—and call this ginormous number Ω, then the absolute entropy can also be described as S = kBlnΩ, where kB = 1.38×10−23 J/K is the Boltzmann constant (note that it has units of entropy), and ln() is the natural logarithm function. This relation is inscribed on Boltzmann’s tomb.
It is this amazing relationship that forms the foundation of statistical mechanics, by which classical thermodynamics can be understood as the way energy distributes among microscopic states in the form of velocity distributions, collisions, vibrations, rotations, etc. Intuitively, the more ways energy can tuck into microscopic modes of motion, the less apparent it is to the outside world in the form of increased temperature. A system with deep pockets will not increase temperature as much for a given injection of energy. Substances with higher heat capacities have deep pockets, and therefore more ways to spread out the energy internally. The states of these systems require a greater amount of information to describe (e.g., rotational and vibrational modes of motion in addition to velocities, intermolecular interactions, etc.): they are a mess. This is the origin of the notion of entropy as disorder. But we must always remember that it is in the context of how energy can be distributed into the microscopic states (microstates) of a system.
Informational Entropy
The fans went wild. In 1949, Claude Shannon was characterizing information loss, and needed a term for the degree to which information is scrambled. Visiting mathematical physicist John von Neumann, he received the following advice:
You should call it entropy…nobody knows what entropy really is, so in a debate you will always have the advantage.
Gee, von Neumann couldn’t have been more right. The resulting duplicate use of the term “entropy” in both thermodynamic and information contexts has created an unfortunate degree of confusion. While they share some properties and mathematical relationships, only one is bound to obey the Second Law of Thermodynamics (can you guess which one?). But this does not stop folks from invoking entropy as a trump card in arguments—usually unchallenged.
But informational entropy does not generally transfer into the thermodynamic realm. A deck of cards has the same thermodynamic properties (including thermodynamic entropy) no matter how the cards are sequenced within the deck. A shuffled deck has increased informational entropy, but is thermodynamically identical to the ordered deck.
What’s the Difference?
To determine whether two different states of some real or imagined system is meaningfully different in thermodynamic entropy, ask yourself these questions:
- If I took the system to zero temperature and then added energy until getting back to the original temperature, would the amount of energy required be different for the two configurations?
- Is there an intrinsic physical process by which one state may evolve to the other spontaneously? In other words, are the items continuously jostling about and changing configuration via collisions or some other form of agitation?
The first question primarily boils down to whether the microscopic structure has been changed, so that the places energy gets stored will look different before and after. If the change has been chemical in nature, then almost certainly the micro-level energy storage properties will be different. If it’s just a matter of moving macroscopic pieces about, then any entropy change is probably too small to care about.
The second question concerns the relevance of entropic differences, and highlights the notion that entropy only really makes sense for systems in thermodynamic equilibrium. Salt grains and coffee grains sitting in two separate piles on a flat surface will sit that way indefinitely over any timescale we consider to be relevant. Absent air currents or other disturbances, there may be small thermal jostling that over billions of times the age of the Universe could work to mix the two populations. But such timescales lose meaning for practical situations. Likewise, books and papers heaped on the floor have no random process of self-rearrangement, so the configuration is not thermodynamically relevant. Applying the test outlined by the first question above would have the same thermodynamic result in either configuration.
Another way to say this is: it does not make sense to characterize the entropy of a given frozen arrangement. The salt and coffee example, whether mixed or separated (with no barrier between, let’s say) are both equally probable instances of the same system energy. Yes, there are myriad more ways to arrange a mixed state. But a particular mixed state is just as special as the separated piles. If we had a removable barrier between separated piles and provided a random agitating process by which grains could rearrange themselves on relevant timescales, then we could describe the entropy difference between the ensemble of separated states with a barrier to the ensemble of mixed states without a barrier. But we can’t really get away with discussing the entropy of a particular non-thermalized (static) arrangement.
Nitpicky Difference
Okay, after saying that configuration changes of macroscopic arrangements effectively carry no difference in thermodynamic entropy, I will make the tiniest retraction and clarify that this is not exactly true. Going back to the coffee/salt grains example, a system of two species of particles does carry a finite and quantifiable entropic change associated with mixing—assuming some agitating mechanism exists. In the case where the number of grains per unit area is the same for the two clusters, the post-mixed arrangement (occupying the same area as the initial separate piles) has an entropy change of
![]() where kB is the tiny Boltzmann constant, and the N values count the number of particles or grains in group 1 and group 2. Simplifying to the case where each group contains the same number of particles just gives ΔS = 2NkBln2, or about 1.4NkB.
where kB is the tiny Boltzmann constant, and the N values count the number of particles or grains in group 1 and group 2. Simplifying to the case where each group contains the same number of particles just gives ΔS = 2NkBln2, or about 1.4NkB.
In atomic and molecular arrangements, we commonly deal with moles of particles, so that N ≈ 1024 particles (the Avogadro number), and the mixing entropy comes out to something of order 10 J/K (compare to absolute entropy often around 1000 J/K). But dealing with macroscopic items, like grains of salt or coffee, we might have N ≈ 10,000, in which case the entropy difference in mixing is about 10−19 J/K.
So there can be a real thermodynamic difference between the two states, some twenty orders of magnitude down from the gross thermodynamic entropy of the system. Why do I use the words “can be” and not the simpler “is?” Because question 2 comes in. If there is no statistical process by which the particles can thermalize (mix) over timescales relevant to our interest, then the entropy difference has no meaning. If we apply the test in question 1 to the pre-mixed and post-mixed piles, the procedure does not provide an opportunity for random rearrangements, and thus no measured change in system entropy will manifest itself in an observable way.
Some Examples
In order to clarify some mistaken themes relating to entropy, let’s look again at the third paragraph of the post, repeated here:
A narrative has developed around this theme that we take in low entropy energy and emit a high entropy wake of waste. That life displays marvelous order—permitted by continuous feeding of this low entropy energy—while death and decay represent higher entropy end states. That we extract low entropy concentrations of materials (ores) from the ground, then disperse the contents around the world in a higher entropy arrangement. The Second Law warns that there is no going back: at least not without substantial infusion of energy.
Low Entropy Energy?
Characterizing an energy source as high or low entropy makes little sense. Take the Sun, for example. The surface of the Sun is about 5800 K. Every Joule of energy that leaves the Sun removes about 0.17 mJ/K of entropy from the Sun, according to ΔS = ΔE/T. In this way, the Sun’s total entropy actually decreases with time (internally, it consolidates micro-particles: hydrogen into helium; externally, it spews photons, neutrinos, and solar wind hither and yon). So the Sun is a prodigious exporter of entropy. Let’s say we catch this Joule of energy on Earth. When absorbed at a temperature of 300 K, we could say that we have deposited 3.3 mJ/K of entropy. So that Joule of energy does not have a fixed entropic price tag associated with it: 0.17 mJ/K became 3.3 mJ/K. If we cleverly divert the energy into a useful purpose, rather than letting it thermalize (heat something up), the Second Law requires that we at least increase terrestrial entropy by 0.17 mJ/K to balance the books. We are therefore mandated to deposit at least 0.17/3.3, or 5% (50 mJ) of the energy into thermal absorption, leaving 0.95 J free to do useful work. This results in a 95% efficiency, which is the standard thermodynamic limit associated with operation between 5800 K and 300 K (see related post on heat pumps).
The point is that rather than characterize solar input energy as low entropy (little meaning), we should just focus on the fact that we have a large temperature difference between Sun and Earth. It is the large temperature difference that allows a flow of energy from one to the other, and the Second Law allows diversion of some fraction of this energy into a non-thermal path without reducing overall system entropy.
By the way, the entropy of the Earth as a whole, like the Sun, also decreases in the long term, made possible by a net exodus of stored thermal energy and the lightest gases (hydrogen and helium).
The Quick and the Dead
What about the entropy of living vs. dead things? If we drop our notion of which is more or less orderly, and think thermodynamics, it becomes easy. A 50 kg living person has lots of water content. The heat capacity is high. The entropy of this system is large. A dry, decaying corpse, let’s say also 50 kg, has a lower heat capacity, lacking liquids. So the thermodynamic entropy of the corpse is lower than that of the living thing.
This comparison may or may not be surprising, but it wasn’t necessarily fair. The living version of the 50 kg corpse had a larger living mass, and as the water evaporated the entropy of the entire system (tracking all the mass) goes up. It’s just that the solid remains, in a pound-for-pound comparison, ends up at lower entropy. Note that this result does not respect our sense of “order” as low entropy. The presence of lots of improbably operational subsystems in the living organism does not translate to a lower entropy state, thermodynamically speaking.
A related matter is the notion that we eat low entropy food and produce high entropy waste. In this context we associate “usefulness” with entropy—or lack thereof. We can eat a useful burrito, but cannot derive sustenance by eating our solid waste. In a direct comparison, the solid waste (out of which our bodies remove as much water as possible) has lower thermodynamic entropy than the same mass of burrito—since the latter has more water content. Sorry to be gross here, but this makes the comparisons personally relevant. Sure, the system entropy increased in the process of digesting food (e.g., via respirated gases). But the measure of thermodynamic entropy for a “thing” is not a measure of its usefulness.
Mining Materials
The story goes that we extract low entropy (i.e., concentrated) resources from the ground, and turn them into high entropy products. Sometimes this happens, but often it is the reverse. When we pull fossil fuels out of the ground and combust them into several species of gases, we increase entropy. All the king’s horses and all the king’s men will never put fossil fuels back together again. At least not at an energetic bargain.
But let’s look at another common case. Mineral ores are local concentrations of some material of value—like copper, aluminum, gold, etc. The ore is fantastically more concentrated than the average crustal abundance. Our information-entropy minds tag this as low entropy material. But the ore is still far from pure: maybe a few percent of the ore contains the metal we want. The rest is rock we care little about. Our quest is to purify (concentrate further) the material.
First, let’s compare a kilogram of copper ore and a kilogram of refined copper. The ore has low-heat-capacity metal (copper), plus higher-heat-capacity rock. The entropy in the ore is higher than the entropy in the product. So far, no one is perturbed, because the purity, or orderliness, has increased (wrong reason to think the copper is lower entropy, but okay). Now the copper is deposited on circuit boards in small traces and put into cell phones that get shipped around the world, many ending up in landfills. What is the entropy of the 1 kg of copper now, having been strewn across the planet? Thermodynamically, it’s the same. If we somehow contrived the test of adding energy to bring this globally distributed copper from 0 K to 300 K, the amount of energy required (performed quickly enough that we may ignore diffusion into surrounding media) would be the same for the block as for the distributed mass. Macroscopic configuration changes don’t contribute measurably to changes in thermodynamic entropy.
Note that if for some reason I happened to be interested in the material with higher heat capacity—mixed with lower heat capacity material—the process of separating the material would produce a chunk of pure material with a higher thermodynamic entropy than a similar mass of raw material. So it’s not the purification, or ordering, that makes the entropy go down. It’s the thermodynamic properties with respect to how readily energy is absorbed and distributed into microstates.
The other way to look at the ore situation is to take 100 kg of a 1% concentration ore, and separate it into 99 kg of rock and 1 kg of the target material. What is the entropy difference in the original ore and the separated piles? As long as the grain size of the good stuff is semi-macroscopic (well away from atomic scale), then the entropic difference is negligible. If it is chemically mixed at the atomic scale, like if we wanted to extract chlorine from salt, then the entropy difference could in principle go either way, depending on resultant material properties. But the sorting process has negligible impact on entropy.
Interpretation
The context of this discussion is mis-application of the Second Law of Thermodynamics to systems that might appear to exhibit entropy differences in the form of orderliness of macroscopic arrangements of matter. But many of these “intuitive” cases of entropy differences translate to little or no thermodynamic entropy differences, and therefore do not fall under the jurisdiction of the Second Law.
Simpler statements that are consistent with the laws of thermodynamics and bear on our societal options are:
- Energy may be extracted when temperature differences exist (e.g., combustion chamber compared to ambient environment; solar surface temperature compared to Earth surface). Entropy measures of the energy itself are not meaningful.
- Net energy from fossil fuels may only be extracted once.
- Efficiencies are capped at 100%, and often are theoretically much lower as a consequence of the Second Law.
Meanwhile, we should break the habit of invoking the Second Law to point to the irreversibility or even just the energy cost of restoring ordered arrangements of matter (as in mined ores and recycling). Even if the thermodynamic entropy of processed goods is higher than the feedstock (usually not the case, and at best negligibly different), the Second Law is not the primary barrier to reversing the process. As long as 1017 W flows from the Sun to the Earth, physics and entropy impose no fundamental limits on irreversibility. Our limitations are more on the practical than on the theoretical side.
I thank Eric Michelsen, Kim Griest, and George Fuller for sharing insights in a fascinating discussion about the nature of entropy. It is said that when a group of scientists discusses entropy, they’ll be talking nonsense inside of ten minutes. I think we managed to steer clear of this common peril. I also learned from these links.
Views: 4318
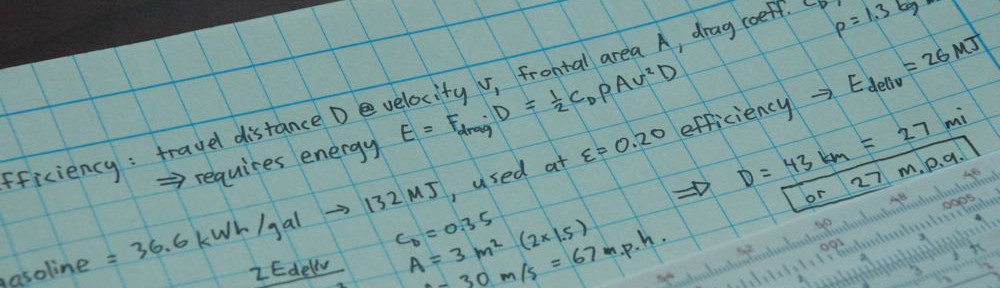


I must admit to being a little baffled by the context of this post. Has someone, with a straight face, argued that the second law of thermodynamics is a reason that we should not or can not recycle?
As much as anything, the post addresses a widespread misuse of entropy to describe macroscopic disorder. But specifically, the branch of ecological economics (whose overall message/drive I support) often uses entropy and the second law in a mushy, incorrect manner. I have not seen statements go so far as to claim recycling is not possible. But the second law is nonetheless invoked—with no quantitative analysis. They don’t need the second law to still have valid points, so should probably drop it to prevent a backfire.
A major instance of this backfire is the thermodynamic handwaver’s dismissal of the idea of capturing CO2 from the atmosphere through enhanced weathering.
Because it is sufficiently exothermic, the Second Law favours it. It increases entropy.
I think a lot of the confusion comes from the analogies used when trying to explain entropy. When I first learned about entropy, the “disorder” explanation was used with analogies very similar to the first couple paragraphs of this post. I was very confused about how disorder could be quantified as J/K until now. Thanks for the clarification!
According to http://entropysite.oxy.edu/, chemistry textbooks are rapidly dropping the disorder analogies. So maybe in 70 years there will be far less confusion on this subject…
Well this is a bit of a strict interpretation of thermodynamics that only has to do with temperatures (to be faire it is called _thermo_ dynamics) and huge numbers of particles and states. However, the fact that when similar things happen in the macro world, they happen at orders of magnitude smaller states, doesn’t mean we should dismiss entropy as a useful concept on that scale. The fact that energy losses of moving macro objects overshadows thermodynamic losses doesn’t mean it isn’t useful to take into account disorder in the analysis of a macro situation.
It would take much more effort for me to sort out mixed salt and pepper than to mix them back up. Sure it doesn’t have much to do with temperature and the number of states is very small compared to what you have in things like gases, however, we can use very similar equations to analyse the disorder so why not do it?
You could even say that the more interesting situations are at a scale in between the macro world and the atomic world. Information patterns in a computer and the electro-chemical patterns that hold knowledge in our brains can be analysed for their order and disorder and their configuration tend to interact with the world in ways that can have huge impact on efficiency and energy use.
Re-sorting the salt and coffee would indeed be a pain in the neck. But one can devise schemes (in theory) that would accomplish the task with almost no energy. So the complexity does not incur a steep energy price, and the Second Law is not what stands in the way. In other words, were you to quantify the theoretical energetic limitations to re-sort the salt/coffee, the number you would get would be so staggeringly small as to be meaningless in any practical sense.
Right, so we may not be calculating absolute energy limits but still using some kind of Shannon information measure give you an idea on the amount of measurements or steps required to perform the task.
The line between the two types of entropy is not that clear. Information is made of matter whether it’s electrons in a computer or chemicals in our heads. In order to have ‘intelligence’ a part of you has to be physically correlated with a part of the world, some particles in your head have to have patterns that approximately and functionally ‘mirror’ part of the world.
Thermodynamics is also about particles having properties that correlate with each other. This means that in a low entropy situation knowing something about a particle tells you something about some other particles.
There is a saying that “knowledge is power”. This is true in a very physical sense. For example, take the thermodynamic textbook example of a container with a gas on one side and void on the other. If there is no barrier between the two side the gas should move to fill the void and settle in the higher entropy case of evenly filling the space. Thermodynamics says that you would need to spend energy to push the gas back to one side.
However, if you were to put a wall in the middle of the container with a little door large enough to let a molecule go through, and you knew exactly the position and velocity of each molecule in the container, you could open and close the door at exactly the right time when a molecule is about to go from, say, left to right through the door and close it when one is about to go right to left. Using very little energy you could get all molecules to end up on one side of the container.
This should violate the second law of thermodynamics but it does not! Why is that you ask? It’s because the knowledge you have about the position and velocity of all these molecules is a source of low entropy. Knowledge is low entropy and the correlation between the particles in your head and the real world is what allows you to make predictions and extract useful energy.
The tiny door experiment is clever, but consider that having full knowledge of the exact microstate of the gas—to the point of being able to deterministically predict trajectories into the future—has deprived the system from being some ensemble of possible states in thermodynamic equilibrium. It is then a single state, perfectly known. It’s not that entropy is reduced by some low entropy knowledge. Entropy has ceased to have meaning, de-fanged of a statistical description. You can’t assign an entropy to a single state: only to an ensemble of states subject to some (quasi-static) constraint and able to freely morph from one state to the next at the same energy. I think you’re walking a dangerous line that still mixes up two physically distinct realms
” but consider that having full knowledge of the exact microstate of the gas has deprived the system from being some ensemble of possible states in thermodynamic equilibrium. ”
an “ensemble of possible state” is a very information theoretic concept that has to do with being ignorant of the actual “micro-state” of the gas. In my opinion, the fact that it is difficult to discuss the details of thermodynamic entropy without implying things about the state of knowledge of aggregate particles is a testament to the equivalence of information entropy and thermodynamic entropy.
I also want to add some references. I am no physicist or mathematician just an engineer who dabbles for fun. However, E.T. Jaynes is the guy who made all this clear in my mind. He wrote a paper “The Evolution of Carnot’s principle” which does a good job of explaining the link between information and thermodynamics.
http://bayes.wustl.edu/etj/articles/ccarnot.pdf
You might want to start with chapter 10 of his unfinished book (http://omega.albany.edu:8008/JaynesBook.html): Physics of “Random Experiments”.
This is a more philosophical discussion of the link between physics and probabilities. It’s useful for understanding the intellectual stance Jaynes is using in the Evolution of Carnot’s Principle paper.
If you are looking for more after that, there are gems in his bibliography http://bayes.wustl.edu/etj/node1.html and unpublished manuscripts http://bayes.wustl.edu/etj/node2.html a lot of which would have made great blog posts would this medium have been available in his lifetime.
You don’t need full knowledge of the microstate. Even one bit of knowledge would reduce the statistical mechanical entropy by ln(2), and in theory this difference can be exploited to extract work (k_b * T * ln(2) Joules) using a contraption like the Szilard’s engine.
More generally, informational and thermodynamical entropy are related by Landauer’s principle.
While these entropies and energies are small compared to typical thermal energy and entropy scales, I don’t think it is wrong to say that the fact that we can’t generally recyle waste back into orderly “useful” materials without an energy expense is fundamentally a consequence of the second law of thermodynamics.
“Re-sorting the salt and coffee would indeed be a pain in the neck. But one can devise schemes (in theory) that would accomplish the task with almost no energy.”
It depends on what you mean by “almost no energy”. If you mean an amount of energy which is small with respect to the absolute thermal energy of the pile, then you are right. If you mean an abitrarily small epsilon, then Maxwell’s demon type of pardoxes would apply.
I’m curious here too. How can be those schemes that can do the re-sorting with almost no energy? I guess that a good reference to compare would be the energy needed to do the mixing. “Almost no energy” in this case should be no (much) more energy than that one.
This article seems like a quibble to me. While the use of the exclusive term “entropy” to describe “disorder” in human-perceived terms rather than in terms of thermodynamics might make physicists jobs a little harder, there is huge value in the layperson having a name for the concept of describing the likelihood of highly-ordered (or low-probability) arrangements remaining that way over time. The term “entropy” is much more palatable than “chaos theory” or “complexity”.
I have no problem with the dual use of the term entropy in colloquial contexts. The problem comes when any facet of thermodynamics is invoked, because thermodynamics has little to say about macroscopic arrangements of matter.
This is interesting, and leaves me still largely confused about Entropy. So, to cut to the chase then, what are the cases in which entropy does matter? In the Save the World sort of situations—oil, consumerism, local food….
I would say that entropy matters in chemical transformations. But it’s so obvious that we hardly need the spooky Second Law to keep our thinking straight: we can’t burn oil twice and get net energy out; or that efficiencies can’t exceed 100%; no perpetual motion. So in large part, I think entropy and the Second Law don’t generally offer deep new insights into common-sense constraints.
Tom, I have a topic request.
Your first summary point, that energy can be extracted when a difference exists, seems very, very important for all sorts of Zero Point Energy and Powered by Vibrations sorts of devices that choke facebook.
The Archdruid did a series of posts on just this, maybe a year ago. But would you mind summing up the reality of the situation as only you can do?
That first summary point might come across as broader than it is intended to be. Energy can be extracted when temperature differences exist, but this is not the only context in which energy may be extracted—it just happens to be the most prevalent one in our world, given all the heat engines about. A moving hammer head can be at the same temperature as the nail, the wood, and the air, but still capable of doing work. Likewise, mechanical vibrations, via some rectification scheme, could do work. Now what drives the hammer or the vibrations is another important layer. Almost certainly it is traced to some thermal difference that was able to promote the flow or capture of energy.
So, AFAIK, Georgescu-Roegen mis-applicated the Second Law of Thermodynamics, -he was one the very first people to make the “ore entropy” statment- and therefore he was wrong in many aspects.
Yes, Georgescu-Roegen was a founding figure in ecological economics, and his thoughts on entropy have remained influential in the field. Many recent references to entropic limitations simply quote G-R as an authority. But what if he didn’t actually understand entropy in the thermodynamic sense? This is why deference to authority is a poor substitute for science.
Absolutely agree. I must admit that I “believed” in an authority such as G-R until I read this post/article. Again scientific thinking wins over authority. I always regarded myself as an skeptical thinker, so I thank you very much for keeping us folks aware from poorly reasoned arguments.
I do not believe that it is correct, let alone fair, to say that G-R misapplied the Second Law. He fully and explicitly recognised its limitations. This is why he proposed his Fourth Law, which may or may not be correct in the strict sense, but certainly seems to be valid for all practical purposes. I.e., if we mix that salt and pepper, their utility to us will be reduced and cannot be restored without energy input, which will also involve a dissipation of matter (loss of salt and/or pepper and/or materials used in the process). Obviously, ‘loss’ is not meant in the strict sense, but in the sense of lost to humanity. I see nothing in this post that would invalidate G-R’s arguments in the context they were formulated and meant to apply. We would not be able to recover 100% of copper from our waste even if we had virtually unlimited energy energy to do so. Or are you suggesting that 100% recycling is feasible?
This is an excellent article!
I have been confronted with 2nd law of thermodynamics arguments and have even “used” it myself when my mother jokingly rationalized my jnability/unwillingness to tidy up my room. This post sheds a lot of light on the subject.
I feel one important thing is missing from this discussion: the nature of the second law. It is not a strict law. Much more very, very unlikely to be violated in thermodynamic settings. One (famous (among statistical physicists)) example is the fact that all the air molecules in this room concentrate spontaneously in the other half of my room (which would reduce the entropy) is not impossible but unbelievably unlikely.
I think one can use “entropy” as a concept on macroscopic scales to compare “entropy” at the same scale and the same agitating mechanism. Comparing shuffling a deck of cards with heating it up is clearly non-sense. But saying that it is very unlikely that a deck of cards will be in any (particular) ordered state after random shuffling because of some macroscopic 2nd law of card shuffling is legitimate. Of course, the orders of magnitude are unbelievably different. (In my opinion – what do you say?)
The key things are equilibrium and agitating mechanism to connect the different levels of macroscopic and thermodynamic entropy. Thermodynamically two macroscopic solid bodies are in equilibrium when the have the temperature but somebody else might argue that equilibrium is reached when the heat death of the universe is reached (but we do not know for sure that this is the fate of the universe).
The case where all particles can (statistically) end up on one side of the room represents one of the myriad equally likely states of the system at the same energy. So it makes no sense to talk about the entropy of that state: it is transitory, and will revert to full-room occupation within milliseconds. The system has the same constraints the entire time, and the entropy is a measure of how many states can satisfy these constraints at a given energy.
We need to break ourselves of the habit (and I too was recently guilty) of ascribing a measure of entropy to some snapshot configuration. It is the ensemble of snapshots that can be characterized by entropy, not any single instance.
Okay, your right! Since such configuration would not be in equilibrium it does not make sense to speak of entropy.
I don’t see why it wouldn’t make sense to talk of the entropy of one side of the room having all the particles – that’s still an ensemble of enormous number of microscopic states even if it is not in equilibrium. You simply lower Ω accordingly and you end up with a much lower entropy. That it will revert back quickly seems to be just a restatement of the Second law.
If you are going to explore an ensemble of all possibilities in which the particles are on one side, then you have imposed a constraint that all particles are on one side, and now have a barrier. Entropy makes sense in the context that the particles can randomly explore all the states being considered. If you are only considering the case when particles are on one side of the room, and not considering occupation of the entire room, then the thermodynamic scenario you describe is one with a barrier. Yes, the entropy is lower in this one-sided ensemble.
But if we’re looking at a random instance of all particles sloshing to one side momentarily as part of the full-room ensemble, then we’ve got one snapshot and not an ensemble.
There are some things I’m still not clear about. Isn’t a “corpse” a single state that the atoms making it up could be in? How can we talk about the entropy of a corpse but can’t talk about the entropy of a bunch of balls lined up on one side of a table? I guess I’m confused as to where and when you can draw barriers when describing a given set of all particles in all their possible states, which I take from this as the meaning of entropy. More states = more random, undirected energy = more entropy?
A second aspect of this that leaves me feeling uncertain is the definition of equilibrium. As I understand it, when a system (which I guess is a set of particles in all their possible states at a given energy level?) has come to equilibrium, it means there is no net change. But net change of what? No net movement of striped balls v. solid balls rolling around on a table? Certainly, if we’re speaking of real particles, they never stop moving. The living organisms on earth are bags of particles that still haven’t reached an equilibrium due to energy still coming in from the sun, correct? While organisms have this influx of free energy coming in, they maintain their compartments and thus can assume fewer possible arrangements of their atoms than corpses can. Turn off the energy and then shrivel up and die, but when can we really say equilibrium is reached and actually start talking about the entropy level? A corpse is just a stopping point on the way back to either new life or complete disorder, right? I agree that the evaporating water from the rotting corpse is taking away a lot of energy…but how does that result in the corpse molecules having fewer possible arrangements than a living one, which I guess would be required to have lower entropy, right? I’m not a physicist, clearly.
Lastly, the timescale of things has me puzzled. A living cell is a collection of atoms and molecules. True, that is just one arrangement of the molecules, but it’s also a very unlikely one. Usually that doesn’t happen randomly, right? (it would never happen randomly – only via lots of time in inputs of energy). When you say that we can’t judge one arrangement, but rather have to look at the whole ensemble of possible arrangements, over what time scale do you mean? How do we know when we have considered enough arrangements that we can evaluate the entropy of something?
limited time for response, but…
The key to entropy is how many ways a system can store entropy. So often we use gas as our example system, that people latch onto configuration as the key. By this logic, solids would have no thermodynamic entropic quality, since the configuration of atoms is fixed. But energy can still hide in microstates of vibration.
Break the habit of associating entropy with configuration alone. It’s how energy gets tucked into microstates.
Thanks, that actually helps. If I think about the entropy of a system as the stored energy of that system in the form of closed feedback loops (particles bumping randomly into each other in elastic collisions, vibrations, absorption and radiation of energy), then I can imagine how entropy rises as heat is added. Adding a little bit of energy to a cold system will create a lot of random motion and rearrangement and switching of configurations. When chemical bonds form and this motion decreases (if endothermic), then entropy decreases. However, to me at least, that seems to argue that a living body would have lower entropy due to all the chemical bonds storing energy and a corpse would have higher entropy if you include the motion of the water that is evaporating (without subtracting an heat transferred to the surroundings, which really is just increasing the entropy of the universe, but came from the corpse). Examined this way, I think it matters what time scale and where we draw our boundaries in answering a question like that.
Thanks so much for clearly laying out this explanation of Entropy. I agree there is a lot of confusion and misuse of the term in general discourse today, which makes most discussion of it meaningless.
In fact I think some of the more interesting aspects of the Second Law of Thermodynamics can be considered without even having to mention the word entropy. I’m interested specifically in how energy flow’s from areas of greater concentration towards areas of less concentration. Can you elaborate on whether there is anything in the Second Law or physics itself which constrains how this occurs?… such as taking the fastest route possible or the most direct path, or perhaps the one that maximizes energy dispersal over a specific time frame?…or perhaps just randomness?
Although it’s merely speculation, I’m interested in the thought that the evolution of matter here on earth (for example) into more highly ordered structures (such as humans, computers etc) is a process not only constrained by the 2’nd law but perhaps could be shown to be, at least partially, a consequence of it? Would love to hear more thoughts on this.
“I’m interested in the thought that the evolution of matter here on earth (for example) into more highly ordered structures (such as humans, computers etc) is a process not only constrained by the 2′nd law but perhaps could be shown to be, at least partially, a consequence of it? Would love to hear more thoughts on this.”
This is explored by Rod Swenson: http://rodswenson.com/ and in the book Into the Cool by Eric Scheider and Dorian Sagan who describe life and spontaneous order in general as ways of speeding up the second law — they more rapidly disperse an energy gradient.
Impressive that you managed to get all the way through that discussion without even an oblique allusion to Maxwell’s Demon.
The other way to look at the ore situation is to take 100 kg of a 1% concentration ore, and separate it into 99 kg of rock and 1 kg of the target material. What is the entropy difference in the original ore and the separated piles? As long as the grain size of the good stuff is semi-macroscopic (well away from atomic scale), then the entropic difference is negligible. If it is chemically mixed at the atomic scale, like if we wanted to extract chlorine from salt, then the entropy difference could in principle go either way, depending on resultant material properties. But the sorting process has negligible impact on entropy.
But in practice, for most ores, it is metals and atomic scale that we’re talking about. So thinking about the process in terms of entropy still makes sense though the clarification is useful.
What about the entropy of living vs. dead things? If we drop our notion of which is more or less orderly, and think thermodynamics, it becomes easy. A 50 kg living person has lots of water content. The heat capacity is high. The entropy of this system is large. A dry, decaying corpse, let’s say also 50 kg, has a lower heat capacity, lacking liquids. So the thermodynamic entropy of the corpse is lower than that of the living thing.
That is correct, but most biologists would not consider the water when thinking about the entropy of a living organism. The entropy of a bunch of C,H,N,O,P and S atoms is much lower when they are organized in a long strand of DNA or a protein than it is if the macromolecules are separated into nucleotides and amino acids, and this is the basis for the thinking of life forms as negative entropy importing devices.
Which reminds of something I did not see in the original post, but I would be curious to see your thinking on – the concept of negative entropy is foundational to a lot of what was mentioned in its beginning, but the rest of the post obviously goes in a different direction, so where does it fit in your thinking?
Do you know about “reversible computing”? Seems like a close connection between information theory and thermodynamics there.
Do you mean quantum computers?
Not the same thing as quantum computing: reversible computing tries to reduce heat dissipation by preserving information. I am not a physicist, but if overwriting bits in a computer’s memory generates heat, it suggests to me that the connection between information theoretic entropy and thermodynamic entropy goes deeper than a von Neumann quip.
See http://en.wikipedia.org/wiki/Reversible_computing .
If the “connection between information theoretic entropy and thermodynamic entropy” went any deeper than being a compelling analogy, wouldn’t we be able to have a digital battery? Imagine a device that has a huge memory capacity, controlled by a small storage program that shifted successive memory bits from 0 to 1 every time a key was pressed. From a starting state in which all bits are at 0, after 1 million key presses, there would be a million bits at 1.
If we could release those stored 1 bits — arguably “information” — by switching them all back to 0, would we have a flow of energy that could be tapped for some work?
Note that we could certainly imagine a much higher number of 1 bits – millions of millions in today’s storage devices. As a follow-up, would it make any difference if we eliminated the “input” energy expended by someone pressing a key many times, by writing a routine to simulate key presses to the storage program?
If you can make a battery out of this, head for the patent office. I’m sticking to understanding entropy as used in information theory as an analogy from physics, one with the demerit of causing confusion by tempting us to extend our analogizing with other laws and observations of physics.
I don’t really understand what you have in mind, but it seems that you are describing a completely deterministic process.
Deterministic processes have zero informational entropy.
[Comment shortened in keeping with discussion policy; removed equations/development that failed to format]
You need to go back to how Gibbs derived thermodynamics form statistical mechanics in order to understand where you are confused. Here is a link to Gibbs 1902 book:
http://www.plouffe.fr/simon/math/Gibbs%20J%20W%20Elementary%20Principles%20Of%20Statistical%20Mechanics.pdf
[… removed material …]
Gibbs is the first to present this relationship on page 33 of his book, equation (88).
The first two laws are just statistical properties of a symplectic manifold of Markovian processes. We use these relationships in many other applications, such as (Markov Chain Monte Carlo) MCMC methods the logarithm of the Hastings Ratio, leads to a difference in the index of probabilities. Jaynes (2003) uses this to define an acceptance criteria as Bayesian hypothesis testing. By accepting the hypothesis with the highest absolute value of the index of probability we are looking for the distribution that has the maximum entropy based on the constraints and data provided.
I hope to impress upon you the simplicity of what entropy actually is. Entropy is the measure of our uncertainty of a system. We express our knowledge of the system as a probability density function. Jaynes has a seminal book “Probability Theory: The Logic of Science” that is well worth the read. Only when we look at entropy from an information theoretic standpoint, the generality and power of thermodynamics become apparent.
To my way of thinking, moving material up the concentration gradient (i.e. refining pure metal from ore, making reverse osmosis water from sea water, keeping sodium ions on one side of a cell membrane, or compressing a gas), or increasing order (like the molecules in a fridge vibrating less with cooling, and in the case of the LHC being less energetic than the background temperature of the universe) create local, statistically less probable states. Energy in the form of work is required to achieve this increase in local statistically improbable concentration or order, with a necessary export of waste heat elsewhere. The local order can only be created by expending energy and exporting waste heat = disorder. More dispersed minerals in lower grade ores require more energy to move up the concentration gradient. If you don’t like the use of terms like negative entropy/exporting entropy, would you agree with “the embodied energy of the order of a pure metal or a cold refrigerator with its associated thermodynamically unavoidable exports of heat/waste” is equiavlent to “local entropy reduction in the form of statistically improbable macro order with an increase in the entropy of the universe as whole”.
I’ve heard of this used for embarrassing many a PhD candidate in oral examinations. There are many devices and contraptions where when you shake they go into a microscopically more ordered configuration. You shake the contraption, and viola! Entropy has been decreased! Explain that! It stumps many a student (and quite a few faculty too!)
Generally these situations find a lower-energy state. Shake a box of different-sized pebbles and the big ones rise (little pebbles fall through cracks and the center of mass can accordingly move downward giving up potential energy). Entropy is a measure of how many states pertain to the same total energy. Throw in an energy landscape and you can forget about a consistent description of entropy.
Again, it is key to recognize that macroscopic ordering/sorting is generally unimportant in relation to thermodynamic entropy.
Still, if we go back to the sustainability question – is the entropy of our current civilization lower than the entropy of what we had when we were hunter-gatherers? And is it decreasing with economic growth?
Despite all of what you said, as correct as it is, it would still seem to me the answer to both questions is positive
I find some fundamental issues not, or not being correctly being addressed in this post:
1) that entropy and the 2nd Law would be different things – they are not. In terms of entropy, the 2nd Law is formulated as follows:
“In any process by which a thermodynamical system is in interaction with its surroundings, the total change of entropy of system and surroundings can never be negative. If only reversible processes occur, the change of entropy is zero; if irreversible processes occur also, it is positive.”
In the article the expression “total change of entropy of the system” is used, while the word “total” should refer to system and surroundings together. To consider the change of entropy of a system only, as is done here, does not give a correct description of the phenomenon.
2) that entropy should have anything to do with disorder. The author seems to give an other view, close to the correct one, but doesn’t spell it out, namely that entropy is a mesure for the dispersion of energy only, not having anything to do with disorder. However, when order in a disorderly system is restored, work must be done to do it, but that work disperses as heat in the surroundings, thus increasing the entrppy of the latter, while that of the system remains unchanged (if it has any entropy at all – e.g. shuffled cards have not). How much work depends on the method used, so there is no connection between entropy and disorder.
3) to say that it is meaningless to talk about low- or high-entropy energy, is definitely wrong. Energy technology is about increasing the entropy of the surroundings, by spreading out the energy of a low-entropy source (high energy-density) into the surroundings, where that energy comes on the high-entropy level of those surroundings, being at ambient temperature (low energy-density).
The higher the entropy of an energy source is, the less we can increase it more to that of the surroundings, manifestating itself in a lower, or very low efficiency. Therfore, solar, and most of all wind power, have no economical viability for use on a large scale (wind is on close to ambient entropy level, i.e. spread out in the surroundings already, solar to a lesser extend, due to temperature differences).
In essence, the 2nd Law says that it is impossible to build an ideal machine (no irreversibilities occurring), by which the change of total(!) entropy would become zero.
I could say a lot more, but then this reply would become too long, so I leave it with this.
Uh… I am not sure I follow the math: “start the material out at absolute zero temperature … all the little pieces ΔS = ΔE/T, ” Starting at T=0?
Hi, I understand that using thermodynamical entropy to explain the difficulty of time-reversing macroscopic dynamical processes (such as ore extraction or death of a living being) is not correct and that this is due to a misunderstanding of entropy. However I think it is also dangerous to completely detach Shannon (or information) entropy from thermodynamic entropy. And it is even more dangerous (since it is wrong) to dismiss Shannon entropy as the entropy of one configuration, as suggested in your post. Shannon entropy is related to a distribution, or equivalently to an ensemble, exactly as thermodynamics entropy in statistical mechanics. It makes no sense to compute the Shannon entropy of a configuration of a deck of cards. Moreover, the main difference between the thermodynamic entropy and the information entropy of an ensemble of heaps of salt&pepper, is in the number of degrees of freedom involved, order 10^23 for thermodynamic entropy, order 10^3 for salt&pepper. Energy enters into the picture by weighting the different configuration in the ensemble, it could be assigned also to the Shannon entropy, if the decks of cards had different probability related to some kind of “macroscopic” energy. By the way, when you say that <> it is again a quantitative fact (price is small), but qualitatively computation has a thermodynamic price as well known from the works of Rolf Landauer and many others.
So, shuffling a deck of cards, or tidying a room, require computation by an intervening intelligence; and this computation increases entropy of the universe of a whole in addition to the physical work being done to the cards or room. Any efforts to create local perceived order must necessarily increase overall entropy.
You don’t have to assume the action of an intelligence.
Consider a machine which takes a shuffled deck of 52 cards and sorts it back to the factory order.
What is the minimum amount of energy that this machine has to radiate, hence to consume, to accomplish this task, averaged over the 52! possible permutations of the deck?
The macrostate “shuffled deck”, that is, the uniform probability distribution over the 52! permutations, has log_2(52!) ~= 225.58 bits of informational entropy. A deck ordered in the factory order (or any other fixed order) has zero bits of informational entropy.
According to Landauer’s principle, in order to destroy these 225.58 bits of informational entropy, the sorting machine has to increase the thermodynamical entropy of its surrounding environment by 225.58 k_b ln(2) ~= 2.16 × 10^-21 J / K.
If the machine exports entropy by radiating waste heat to an environment at T = 300 K, then it has to radiate, and hence consume, at least 6.48 × 10^-19 Joules of energy.
This is an extremely small amount of energy, about the same energy of a single photon of visible light. Any practical machine we can devise with current or foreseable technology would have energy requirements orders of magnitude higher than that. That’s why Landauer’s principle is currently not considered technologically relevant, not even for modern computers.
The heat capacity of water is itself a minimum at body temperature (~ 37 deg C), and the heat capacity of water increases on either side of 37 deg C. http://www.engineeringtoolbox.com/water-thermal-properties-d_162.html
Human life happens when the “pockets” are shallowest, and “microscopic modes of motion” are relatively few in water. The energy cost of keeping a body at 37 is minimal, and the free energy available to make proteins/DNA etc maximal.
Then there’s the extremophiles…
Thanks for the great post.
Most lifeforms on the planet don’t happen to sit at this magic 37 deg (need to check its specialness out), including successful beasts like cockroaches and ants that will surely outlast our fragile species. I doubt humans (or any 37 degree animal) would be considered to be minimal energy machines, in any case (even scaled to mass, area, or whatever metric). Could be wrong, but all this smacks of our usual conceit of elevating humankind to some sort of cosmic perfection. I know we’re proud of ourselves, but does it really bear out?
Mammals typical body temperature is in the 36 – 38 C range, birds are in the 40 – 42 C range. Both classes have exceptions: various species have inactivity or hibernation modes where metabolism and thus body temperature drops.
Other lifeforms stay at or slightly above room temperature.
Tom, is this better?
A narrative has developed around this theme that we take in low entropy energy (solar photons, gravitational energy, stored solar energy in chemical bonds and radioactive decay of stellar products) and emit a high entropy wake of waste (infrared photons, smaller molecules, lighter fission products). That life displays marvelous order (is a dissipative system far from thermodynamic equilibrium) — permitted by continuous feeding of this low entropy energy (if we stop eating exergy we die but we also die eventually because the genetic material which drives the continual reconstruction and repair deteriorates) — while death (inevitable) and decay represent higher entropy (not to the bacteria which feed on us causing the decay) end (not really end states but just some other states) states. That we extract low entropy concentrations of materials (ores) from the ground (concentrated by the interplay between the four fundamental forces and available energy), then disperse the contents around the world in a higher entropy arrangement (less exergy). The Second Law (tells us that these processes are irreversible) warns that there is no going back: at least not without substantial infusion of energy.(all the energy in the universe cannot reconstruct Napoleon from the scattered bits, could it?)
The problem is that on many of these items, the second law is silent, because the thermodynamic entropy is barely budged, if at all, by many of these activities. And even when the second law does apply, things can (theoretically) be patched up nicely with a bit of energy input, and the second law is fine. So irreversibility is rendered mute with a bit of energy input, on theoretical grounds.
I’m fully sympathetic to the real practicalities of marshaling scattered or disordered resources. But my main point is that nine times out of ten, the second law should be left out of the argument. It’s just not that spooky.
maybe talking about exergy is better. That gets used up (as entopy increases?). But isn’t that a property of the second law.
Biological example : suppose the salt and pepper are both water soluble. I know that pepper isn’t, so substitue another salt for the pepper in this example.
Now, I have a bag full of salt (NaCl) and a bag full of another salt (suppose it’s KCl). I have a semi-permeable membrane between the bags. I built a molecular sieve using nanotechnology (meaning I borrow from nature the coding sequence for an ion channel and insert the relevant gene in an e-coli or some other host to manufacture it) that only allows potassium through to the bag containing sodium, and only allows sodium through to the bag containing potassium. I built this sieve to extract energy from the process of the ions flowing through the gradient.
Since the situation starts with one bag containing no sodium, and the other containing no potassium, I can extract useful work from this process. Second law means that if I want to reverse this situation, I have to pay a MINIMUM energy cost to reverse this situation equal to the useful work extracted from the process.
This is the same example as you gave above. If it isn’t the Second Law causing this situation, what is?
This is why we cannot remove the CO2 in the atmosphere and trap it permanently in hydrocarbons again without paying AT LEAST the energy cost of all that energy we obtained from burning hydrocarbons in the first place.
Yes, the scenario you illuminate exhibits thermodynamic properties of a system with static constraints. The fluid medium provides random motive mechanism to move the atoms around. The two separated ions will mix, and will not spontaneously evolve to an equilibrium in which they remain separated. Thermodynamic entropy is at play, and the Second Law governs. Note the elements present in this example that were missing in the salt/coffee grains example: motive mechanism; microstates; fixed constraints; ensemble of possibilities explored by thermal jostling on a relevant timescale.
I also agree with the CO2 statement (akin to my rule in the post that we only get to derive energy from burning fossil fuels once). These atomic-scale rearrangements change the way thermal energy can be stored into microstates (thermodynamic entropy) in a way that disordered books and papers in a room certainly do not.