[An updated treatment of some of this material appears in Chapter 6 of the Energy and Human Ambitions on a Finite Planet (free) textbook.]
Part of the argument that we cannot expect growth to continue indefinitely is that efficiency gains are capped. Many of our energy applications are within a factor of two of theoretical efficiency limits, so we can’t squeeze too much more out of this orange. After all, nothing can be more than 100% efficient, can it? Well, it turns out there is one domain in which we can gleefully break these bonds and achieve far better than 100% efficiency: heat pumps (includes refrigerators). Even though it sounds like magic, we still must operate within physical limits, naturally. In this post, I explain how this is possible, and develop the thermodynamic limit to heat engines and heat pumps. It’s a story of entropy.
Entropy, Quantified
Whole books can be written about the gnarly properties of entropy. Put simply, entropy is a measure of disorder. Strictly speaking, entropy is all about counting the number of quantum-mechanical states that can be occupied at a certain system energy. In this sense, the total entropy of a system is S = kBln(Ω), where Ω is the number of states available (a rather large number), ln(x) is the natural log function, and kB is the Boltzmann constant, having a value of 1.38×10−23 J/K (Joules per Kelvin) in SI units.
Okay, that’s deep and cool, but let’s not bog ourselves down counting states. The main purpose of the previous paragraph is to indicate that entropy has a fundamental prescription, and that it carries actual units. Mostly entropy is discussed in a hand-wavy way, but it can be pinned down.
Change Heat: Change Entropy
More relevant to our discussion is the thermodynamic result that if we add/subtract thermal energy (heat) to/from a thermal “bath” (large reservoir of thermal energy, like outside air, a body of water, rock) at a temperature T—measured on an absolute scale like Kelvin—the entropy changes according to:
ΔQ = TΔS
We read this to mean that adding an amount of heat (ΔQ: negative if removing heat) will result in a concomitant increase in entropy (decrease if negative) with the bath temperature as the proportionality constant. Looking at this equation, the units of J/K for entropy (S) should make more sense.
Wait a minute! Did I just allow for the condition that entropy could decrease? Isn’t one of the fundamental rules of thermodynamics that entropy can never go down?
Almost right. The entropy of a closed system cannot decrease. But it can easily decrease locally at the expense of an increase elsewhere. You can re-stack books on the shelves after an earthquake, restoring order. But via exertion, you transfer heat to the ambient air in the process—increasing its entropy.
Moving Heat
A heat pump, rather than creating heat, simply moves heat. It may move thermal energy from cooler outdoor air into the warmer inside, or from the cooler refrigerator interior into the ambient air. It pushes heat in a direction counter to its normal flow (cold to hot, rather then hot to cold). Thus the word pump.
So let’s imagine I have a cold environment at temperature Tc and a hot environment at Th. Cold and hot are relative terms here: the “hot” environment could be uncomfortably cool—it just needs to be hotter than the “cold” environment.
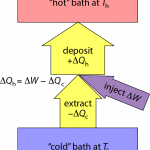
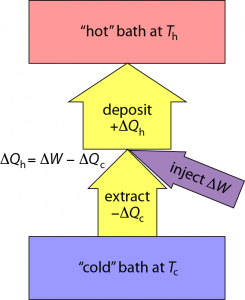If I pull an amount of heat, ΔQc out of the cold environment and put it into the warmer environment, I reduce the entropy in the cold region by ΔSc = ΔQc/Tc. Both ΔQc and ΔSc are negative in this case.
Inevitably, I have to run some machinery to affect this flow of heat against the natural gradient (pushing heat uphill). Let’s call the amount of work (energy) needed to force this thermal extraction ΔW. That mechanical/electrical/whatever energy also ultimately turns to heat, and if I cleverly send this additional energy to the hot place, I end up pumping an amount of heat into the hot environment that is ΔQh = −ΔQc + ΔW (just the sum of the two; as indicated by arrow thicknesses in the diagram above).
The entropy change in the hot environment is determined by ΔSh = ΔQh/Th. Because total entropy must increase, we need the sum of entropy changes to be positive: ΔSc + ΔSh > 0—remembering that ΔSc is negative.
So where does this leave us? If we’re trying to heat a home, we care about how much heat is delivered into the home: ΔQh = −ΔQc + ΔW. And we’d like to do as little work, ΔW, as possible to pull this off. So an appropriate figure of merit is ε = ΔQh/ΔW.
A little algebra with the relations above (the steps are shown in the following graphic) results in the maximum efficiency of a heat pump of ε < Th/ΔT, where ΔT = Th − Tc is the temperature difference between hot and cold baths.
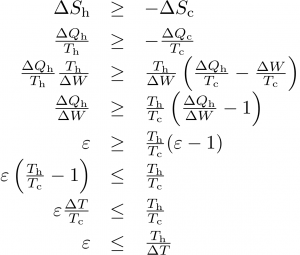If, instead, you want to cool something down (refrigeration, A/C), the figure of merit is how much heat is removed from the cold zone divided by the input work: ε = −ΔQc/ΔW. In this case, the maximum efficiency works out to ε < Tc/ΔT.
Heat Engines
As an aside, if we turn the heat flow around, so that ΔQh flows naturally out of the hot source (ΔQh is negative in this case) and a lesser ΔQc flows into the cold source (positive), the same entropy considerations lead us to derive a maximum amount of work that is extractable from the heat flow, and the efficiency, ε = ΔW/ΔQh works out to be no better than ΔT/Th. (The bolder among you may want to take up the algebraic challenge.) This is the familiar thermodynamic limit for the amount of work obtainable from a heat engine, like a car’s engine, a coal-fired power plant, or even a nuclear plant. The reason we hit a maximum efficiency is really all about not violating the second law of thermodynamics: that the total entropy of a system may never decrease.
Extreme Efficiency
The remarkable thing about the heat pump efficiencies we derived above is that ΔT is in the denominator! Since T is absolute temperature (Kelvin), typical situations will have T ≈ 300 K, and ΔT often a few tens of Kelvin—leading to efficiencies around 10×, or 1000%!! How can this possibly be true? It seems like a total cheat on nature.
The key is that unlike an electric coil or a flame, the heat pump does not create the thermal energy, it moves thermal energy that already exists. A heat pump is always moving thermal energy from a cooler environment to a warmer one. That means that a heat pump heating a house in the winter is grabbing heat from outside and shoving it inside. This may seem counter-intuitive, but I assure you, even freezing air has plenty of thermal energy, being hundreds of degrees above absolute zero. Capturing some of that energy and moving it can take a lot less energy than creating it directly.
One aspect of heat pump efficiency worthy of note is that the theoretical limit gets better as ΔT gets smaller. So a refrigerator in a hot garage will not only have to work harder to maintain a larger ΔT, but it becomes less efficient at the same time, compounding the problem. Likewise, heat pumps operate more efficiently in mild-winter climates than in extreme arctic zones. For instance, the theoretical efficiency of a heat pump operating between 293 K indoors (20°C, or 68°F) and freezing outside is 293/20 = 14.7, while a frigid −20°C (−4°F) would only allow a theoretical efficiency of 7—half as good.
COP and EER
If shopping for heat pumps, one should look for the specification called the Coefficient of Performance, or COP, which is essentially the same ε = ΔQh/ΔW metric from before. Realized values are typically around 3–4. This is a factor of several below the theoretical limit, as is so often the case. But still, it’s rather impressive to me that I can add 4 J of heat energy into my home while expending only 1 J to make it happen (apply any energy unit you wish: kWh, Btu, etc. and get the same 4:1 ratio for a COP=4).
But before we get carried away, let’s say your electricity comes from natural gas turbines, converted to electricity at 40% efficiency (via a heat engine). Coupled with a heat pump achieving a COP of 3.5, each unit of energy injected at the natural gas plant yields 0.4×3.5 units of thermal energy in the home, for a net gain of 40% over just burning the gas directly in the home. I’ll take the gain, but the benefit goes from overwhelming to just plain whelming. If carbon intensity is your thing, then a heat-pump supplied with coal-fired electricity does worse than burning gas directly in a home furnace, since coal generates 70% more CO2 per unit of energy delivered than does gas, eating up the 40% margin previously detailed. We only get the full factor of 3.5 improvement if replacing electric heat.
For cooling applications, one may also see a COP reported. But in the U.S., the efficiency metric is often the Energy Efficiency ratio, or EER The EER. is a freak of nature, and I hope it asphyxiates on its own stupidity. It is the rate of heat extraction, in Btu/hr, divided by the electrical power supplied, in Watts. Geez—Btu/hr is already a power: 1 Btu/hr is 1055 J in 3600 s, or 0.293 J/s = 0.293 W. Why complicate things?! So multiply EER by 0.293 to get an apples-to-apples comparison, arriving at a COP for cooling that corresponds to our measure from before: ε = −ΔQc/ΔW. Air conditioners getting EER values above about 11 qualify as Energy Star, corresponding to a COP above about 3.
My Fridge Performance
I had a thought that I could test the > 100% efficiency delivered by a heat pump by watching my fridge go through a defrost cycle. The idea is that a bunch of heat is dumped into the coils periodically to melt accumulated ice. I noticed that the first cooling cycle after the defrost is always longer, as the deposited heat must be removed.
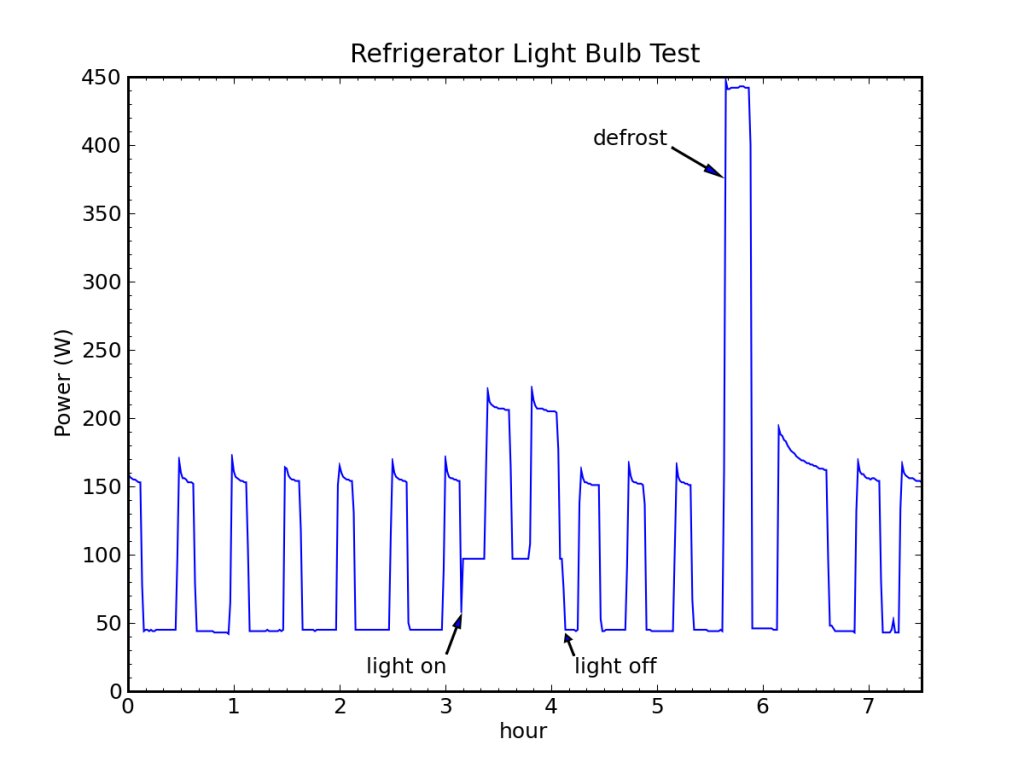
My fridge normally runs on an off-grid stand-alone photovoltaic (PV) system, and I record the system energy expenditures at 5 minute resolution. I see defrost cycles routinely in the data (every day or two). But because of the coarse sample rate and the indirectness of the measurement (measuring battery current, not AC power), I prefer to use TED (the energy detective) data, when available. During unusually cloudy periods, the PV system switches over to utility input, in which case the fridge is monitored by TED and I get one minute samples of direct AC power. One such sequence is shown for my fridge in October, 2011.
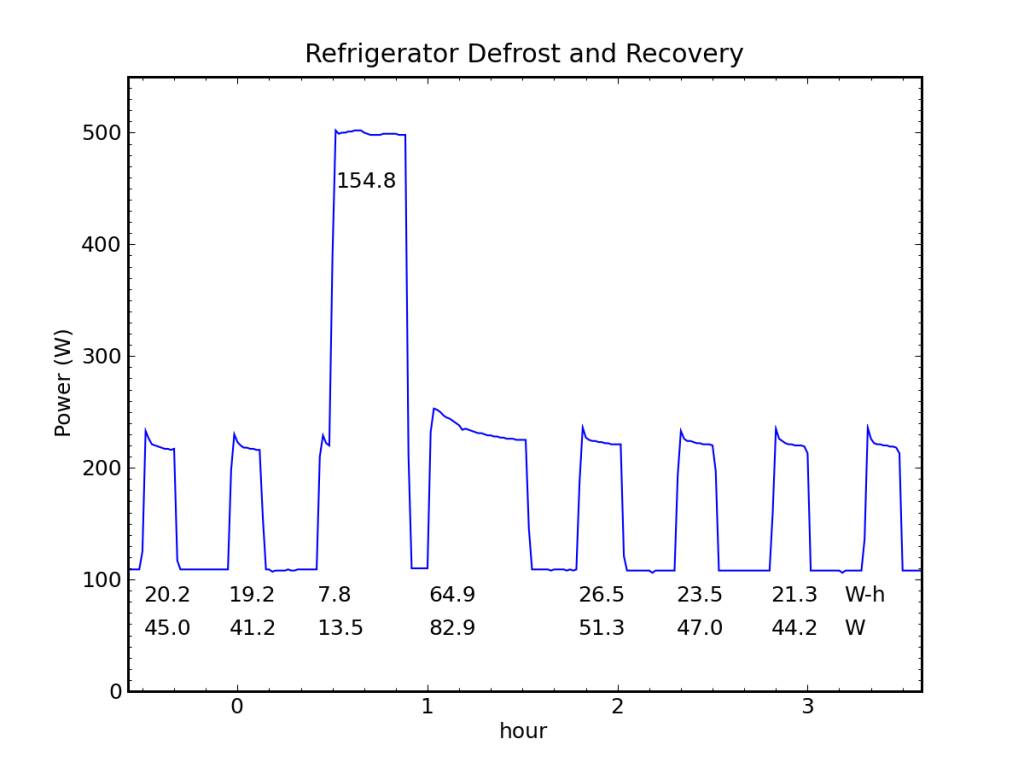
A prominent defrost cycle consumed 155 Wh of energy. The energy and average power associated with each cooling cycle is also shown.
We can see in the figure above a baseload power of 108 W, two normal fridge cycles preceding the defrost pulse at 12:30 AM (and a partial cooling cycle on its leading edge). The first cooling cycle after the defrost deposit is obviously longer than the rest, and subsequent cycles may be slightly fatter and more frequent. The energy expenditure (above baseline) is reported for each cooling pulse in Watt-hours, as is the corresponding average cooling-cycle power measured from the start of one pulse to the start of the next.
Performing a careful accounting for the energy expended while cooling vs. the energy deposited during defrost, and projecting the rate of power use prior to defrosting (43 W) forward, we find that we would have expected to spend 163 Wh over the time interval between the first cooling cycle and the last (the pre-cycles are 19.7 Wh each), but the actual expenditure cooling was 184 Wh, leaving an extra 21 Wh-worth of cooling (roughly equivalent to one extra cycle). Meanwhile, the defrost activity expended 155 Wh in 23 minutes (400 W). So it took 21 Wh of wall-plug energy in cooling mode to remove 155 Wh of deposited thermal energy, implying a coefficient of performance around 7.5!
Impossibly high, methinks. One problem is that the defrost cycle puts energy into melting ice, which subsequently runs out to a drip pan below the refrigerator. So the refrigerator does not later need to remove this heat: it found another sort of exit. The heat of fusion barrier that must be overcome amounts to 334 J/g (compared to about 20 J/g to raise the temperature of water by 5°C, or ice by 10°C). If the defrost cycle produces two cupfuls of water (about a half-liter) each time, the investment is approximately 50 Wh of energy. This brings the COP estimate down to 5. Additionally, since time elapses after the defrost injection is complete, some portion of the heat no doubt diffuses out from the cold coils to the hot fins before the cooling kicks in.
In retrospect, the defrost cycle is not the best way to experimentally determine the COP—despite the fact that the “experiment” runs all the time without my having to lift a finger.
A More deliberate Experiment
Taking matters into my own hands, I rigged an incandescent light bulb operating on a timer and stuffed in the fridge (in a clip-light fixture). I set the timer to pop the light on from 3AM to 4AM, figuring the fridge would be perfectly quiescent (no door openings, etc. during that time). A couple of long, tapered pieces of wood provided a channel for the cord without compromising the door seal. I shifted the fridge over to utility for the night so TED would catch the action. It took three times to get a good result. “When are you going to take that light out of the fridge?!”
Take One
Initial location of light in upper left of refrigerator volume
I placed the light high in the refrigerator, and shone the light onto aluminum foil on an otherwise empty glass shelf (the foil was to keep direct light off the food below). The data were beautifully collected, but the refrigerator stayed on the entire time the light was on. The bulb was rated at 60 W, and the refrigerator typically runs around 120 W, so instantly I knew the measurement indicated a COP less than 1. Not good.
I presume the bulb was near enough to the thermostat as to elevate the local temperature and fool the refrigerator into staying on the full time. Bet the ice cream got rock hard…
Take Two
This time, the light is lower in the fridge.
I moved the light to a lower portion of the refrigerator, hopefully well-enough baffled that the thermostat would not be impacted. This time, I was foiled by a sleepless wife, who turned on and off all manner of electrical devices during the course of the experiment. The refrigerator itself was not disturbed, and if pressed, I could still identify cooling cycles and extract useful data. Just like in astronomy, crummy nights produce crummy data, and you have to work much harder to get marginally useful results. Better to wait for a clear night, if you can. I could at least see that the fridge cycled this time during the light-on phase.
Take Three
Fool me once, shame on you. Fool me twice, shame on me. Since the saying has no “thrice” aspect, I felt I had no choice but to make it work. Actually, I did nothing different (no straps to confine wife to bed—patience was already wearing thin on the interminable experiment in the refrigerator). But fortunately, a quiet night resulted in a clean dataset.
Light pulse demanded more cooling. Note coincidental defrost at end.
The bulb turned out to expend energy at a rate of 52 W. Subtracting a baseload of 44 W, the first five cycles averaged 35.4 W to keep the fridge cold. The light bulb was on for a bit over 56 minutes, depositing 49 Wh of energy. From the time the light bulb came on until the end of the last cooling pulse before the defrost cycle began (spanning 131 minutes), five cycles totaled 57 minutes of on-time, using 113 Wh of electrical energy. Yet we would have expected 35.4×131/60 = 77 Wh at the nominal rate. Thus the refrigerator consumed an extra 36 Wh of energy to remove the 49 Wh deposited by the light. We calculate a COP of ΔQc/ΔW = 49/36 = 1.36.
Hmmm. Not in the ballpark of 3. It’s bigger than 1, at least—indicating some degree of heat-pump magic. But I am disappointed in the result.
Reflections on the Experiments
My mode of testing certainly deviated from the intended operation of refrigerators. A concentrated pulse of constant heat is not quite the same as putting warm food into the refrigerator. It may also be that the freezer achieves a COP around 3 while the refrigerator volume does not. I would be curious to know how the COP is actually measured. Do we realize similar values in daily operation? After all, the light bulb test fell short. If I average the ice-melt-corrected defrost value and the light bulb value, I get a COP around 3, but I have no solid justification for performing this average.
Alternative tests may include placing a known thermal mass into the refrigerator and seeing how much energy is required to bring it to temperature. Door access is a problem, though.
Close the Door!
While I’m on the subject of refrigerators, how about a quick detour to assess how problematic it is to stand with the door open, or to repeatedly and inefficiently access items within. Should I be irked?
Let’s say the inner refrigerator volume is half a cubic meter (about 17 cubic feet; American freezer + fridge often are in the low 20’s). Air has a specific heat capacity of 1000 J/kg/K. At a density of 1.2 kg/m³, we’re talking 0.6 kg of air, total. And let’s assume a ΔT of 20 K between ambient air and fridge air.
A complete air exchange then costs 12 kJ (3.3 Wh). Even at a COP of 1.0, the refrigerator will remove this amount of energy in 100 seconds at a power of 120 W. It’s a tiny fraction of the daily work of the refrigerator: 0.3%.
A more serious problem is condensation. If the outside air is saturated (100% humidity), containing about 20 g/m³ of water, we deposit 10 g into the fridge. The latent heat of vaporization means that 2257 J are deposited for every gram of water condensing, plus about 800 J to cool the water down. In total, we drop another 23 kJ (6.5 Wh) of energy into the fridge.
So depending on how moist the air is, we may drop anywhere from 12–35 kJ. Our 0.3% becomes a 1% effect. Open the fridge 20 times in a day, and you might have a significant issue.
Another consideration is that each door opening may trip the thermostat before it ordinarily would have been. In doing so, the cooling “schedule” advances forward, and could result in more “on” activity than would otherwise occur.
Parting Perspective
Heat pumps are really cool, and seem to violate our sense that 100% is the best efficiency we can ever get. Cooling applications have little choice but to use heat pumps, as cooling inevitably involves getting rid of (moving; pumping) thermal energy. Heating applications can see a factor of three or more increase in efficiency over direct heating. Increasingly, the stable thermal mass of the ground is used as the “bath”—often erroneously referred to as geothermal.
So I’m generally a fan of seeing more use of heat pumps. Replacing direct electrical heating with a heat pump is a clear win. Replacing a gas furnace with a heat pump is a marginal win if your electricity comes from gas; not so much for coal-derived electricity. But heat pumps pave the way for efficient use of renewable energy sources, like solar or wind. In this sense, getting away from gas furnaces while promoting non-fossil electricity generation may be the best ticket—especially when coupled with concerns over global warming.
Views: 12825
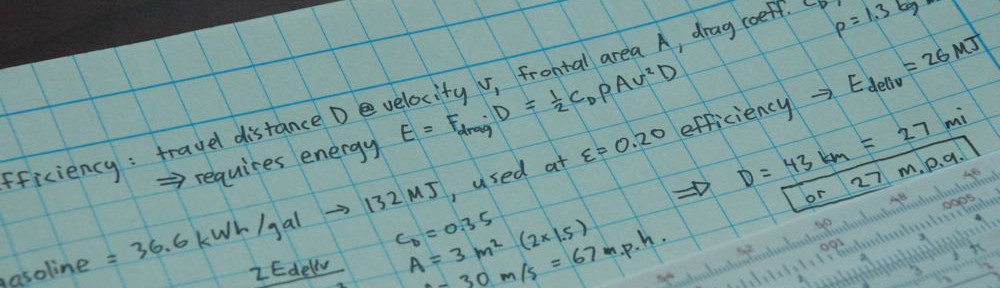
Heat pumps used for cooling will typically have a COP about 1 less than that of those used for heating simply because the power expended in their operation doesn’t contribute to what is considered the good result. So if a typical heating heat pump has a COP of 3 you might hope for a COP of 2 for your fridge.
This is implied by your description earlier on in the article but doesn’t seem to get carried through explicitly to later parts.
Thanks for pointing this out. Right—this can be seen in the diagram since the COP is effectively the ratio of arrow widths. Depending on whether you care about ΔQh or ΔQc, the ratio to the input, ΔW, looks better for heating than cooling. Mathematically, since Tc is always less than Th, the cooling COP: Tc/ΔW, is always less than the corresponding COP for heating: Th/ΔW.
There is the issue of comfort. Gas heat, to me, is more comfortable than a heat pump because the heated air that comes out of the register is warmer and it seems that, in our area, gas heat is less expensive than electric. Our electricity is generated by a mix of hydro, gas, coal, and nuclear.
That’s a question not of the heat source, but of the mode of delivery.
I’ve spent some time living on islands that have mains electricity but no mains gas. Older buildings use oil, newer buildings have electric heaters.
When you discuss changing to heat pumps with the people with electric heating, the system that’s considered is usually a ground-to-air or air-to-air heat pump – something analogous to an office air conditioning unit, except that it blows hot air rather than cold. People don’t like having hot air blown at them, and thus would rather stick with their electric radiator.
But it doesn’t have to be that way. A ground-to-water or air-to-water heat pump system heats water rather than air, and then circulates the water through conventional radiators. I’m not sure how much of an efficiency hit this causes (since some heat will be lost from the pipes rather than making it to the rooms you want heated), but it’s a much nicer way of heating a home. However, if you don’t already have a wet heating system (pipes and radiators) it’s much more expensive to add this than an air-based system.
For the people with oil-fired wet heating, they already have the pipes and radiators and a x-to-water heat pump system is a no-brainer.
Hmm. Sorry. On reflection I had misred your comment, and what I said didn’t actually respond to it!
However, in the parts of the world where wet heating systems are common, the “how hot is the air” question is moot.
And yes, at least in the UK gas is usually cheaper at present. Heat pumps only become a no-brainer if you are using electric or oil-fired heating.
As an aside, I wonder whether there is a useful way that heat from gas could be used to run a heat pump rather than just being vented into the room, to improve the CoP of gas heating? In the same way that older camping vehicles used to have gas-powered fridges? I have little idea of how they worked and no idea what the efficiency was like…
Nice work and nice post, as usual. But please oh please, don’t put deltas on your Qs! What on earth would “change in heat” even mean?
ΔQ is standard practice. A body contains some fixed, measurable amount of thermal energy. Take some of that away, and you have changed it’s thermal energy by some amount, ΔQ. Think of Q as thermal energy, rather than “heat” per se. Energy is an amount that can be changed.
There are competing standards, so why not use the one that actually makes sense? That is, use Q, not ΔQ, for the amount of heat transferred. But I’ve never heard of a standard where the symbol Q stands for thermal energy content, and that’s not how you’re using it because you’re talking about processes where there’s also work being done. Of course, ΔW (change in work?) is just as offensive as ΔQ.
Hi Tom,
Dan makes an important point here. Here’s a quote from ch. 1, Definitions, of the first edition of Joseph Keenan’s classic 1941engineering thermodynamics text, ‘Thermodynamics’:
“Heat is that which transfers from one system to a second system at lower temperature, by virtue of the temperature difference, when the two are brought into communication. It is measured by the mass of a prescribed material which can be raised in temperature from one prescribed level to another.
Heat, like work, is a transitory quantity; it is never contained *in* a body.”
I’d strongly disagree that ΔQ is standard practice in engineering thermodynamics, which is most relevant to the post topic. I’m wondering if the issue might have come up due to someone flying a bit fast and loose somewhere with “d”, “δ” and “Δ” in their definition of entropy i.e. dS = (δQ/T)rev. c.f. your ΔQ = TΔS.
(Sorry to be making my first comment one of this nature–I greatly appreciate your work here).
With best wishes,
Josh Floyd
Its standard practice to use ΔQ in physics, as he is a physicist its not surprising he’d use that notation
Ahem. Some of us are also physicists who can speak with some authority on such “standards.” While it is unfortunately common to write dQ and dW (often with a slash through the d to indicate the “inexact differential”) for infinitesimal amounts of heat and work, I can’t think of any textbook or other standard reference work that uses the notation ΔQ or ΔW for non-infinitesimal amounts. I’ll concede that there must be authors who have used this notation, but it is certainly not the standard. The most common notation for a non-infinitesimal amount of heat or work is simply Q or W.
Can you talk about COP from a Ground Source heat pump.
Excellent article!! I have always been a fan of heat pumps. You did ratchet down my enthusiasm for chest refrigerators though; I thought not exchanging the air would do better than 0.3% improvement.
One thing you didn’t address is gas-powered heat pumps (e.g., propane refrigerators). I’m curious how they would compare. I also am curious about how much of a benefit consumer cogeneration is (i.e., a natural gas powered electric generator in a home that is normally only run when heat is needed.) But that probably would be a whole other article.
About gas-powered heat pumps (like those used in an RV fridge): Wikipedia says that they are approximately on par with a generator+compressor combination in terms of primary fuel used.
I always wonder why there are no AC units based on that principle. All that would be required is concentrating some solar power on the hot end. Maybe the difference between shade and full sunlight would even suffice for the hot and medium heat baths.
I live in New Zealand, and we are lucky (?) in that 70% of our electricity is from renewable sources (hydro, geothermal and some wind), so heat pumps make a lot of sense. I don’t know about comfort – our heat pumps warm our house marvellously, but that also might be that our winters are not so very cold anyway (rarely gets close to freezing) which also helps heat pump efficiency. Also you get a “free” air conditioner for the summer.
I expect that heat pumps will be even more effective when they’re interconnected.
For now, the refrigerator pulls heat out into the room and the air conditioner pulls heat out of the air inside the house and expels it to the outside air. Then, your water heater has to turn energy into heat inside the water heater. You know, that thing which heats water with a COP of, at best, 1.0.
Does anyone else see where this is going?
I expect that, at some point, a house will have a thermal bus or something similar to that. The refrigerator will pull the heat out of its interior and put it into some kind of working fluid. So will the air conditioner. The water heater will take the heat from the working fluid and put it into water. This way, the > 1.0 COP of a heat pump works in all cases.
You may be able to add some phase change material to store heat. You would have some kind of outdoor unit which could collect heat from outdoors, when needed, or dispose of it.
Add in a solar collector, if you wish. It would help, but it wouldn’t be necessary for the rest of the system to work.
Nice concept in principle, but i suspect the devil is in the details. Some that come to mind are the fact that you would probably want this heat reservoir in the house to be significantly above ambient temperature, and that makes any heat pump which tries to cool from it less efficient. Also heat and cold tend to be required at completely different times of the year, requiring that buffer to be bigger than about 6months.
That is a very interesting idea.
You might also want to tie the working fluid into a floor heating system (instead of wall rads or forced air).
I have read that someone put a version of this into practice: the heat pump takes heat out of the house and puts it in a pool. Another takes it out of the pool and puts it in a hot tub. If the hot tub gets too hot, a waterfall is turned on to cool by evaporation.
You would need 2 buses: one for cold and one for warm, just like water pipes.
But I guess this makes sense only in larger buildings, not houses.
Do you know about the work of Shwetak Patel, CS and Electrical Engineering professor at University of Washington?
His lab is working on energy sensors for household energy monitoring.
http://ubicomplab.cs.washington.edu/wiki/Main_Page
Hi Tom,
Thanks for your terrific discussion of heat pumps, this is as always a very clear and accessible overview.
Just a note on your aside about heat engines. You closed that discussion by noting that “The reason we hit a maximum efficiency is really all about not violating the second law of thermodynamics: that the total entropy of a system may never decrease.” While I appreciate the point you make, there’s an element of tautology there. The physical basis for this is, despite the philosophical confusion that abounds in relation to the second law and the entropy concept, rather prosaic. It relates to the fact that heat engines work on a cyclic basis, and that the working fluid must therefore return to is initial state at the end of the cycle in order for the engine to continue operating. If we’re interested only in providing a single “batch” of work output from a single “batch” of heat (e.g. heat a quantity of air, remove the heat source, then allow it to expand against a piston), then it is in principle possible to approach 100 percent conversion efficiency. It’s the heat rejection and additional work required to get the working fluid back to its starting point that imposes the maximum (Carnot) efficiency limit. For any or your readers interested in following up further, I wrote about this recently here: http://beyondthisbriefanomaly.org/2012/04/26/accounting-for-a-most-dynamic-universe-part-3/#entropy
Incidentally, there’s also a link in that post to an article published in the journal Futures looking at the confusion associated with the admittedly rather popular view that “entropy is a measure of disorder” (and that it has anything to do with “messy desks” only in the very loosest metaphorical sense). For reference, Frank Lambert (Emeritus Prof of Chem at Occidental College in LA) has been instrumental in introducing energy dispersal in place of disorder as the basis for understanding the physical phenomenon measured by entropy–his work in physical chemistry education is foundational to the discussion of the second law and entropy in that article and throughout the blog linked to above.
With best wishes,
Josh Floyd
I’m disappearing from the wired world for a bit. Please keep comments coming, but you’ll have a substitute moderator, and questions for me will lie on the floor.
Thanks for that post. I have a very quick question. Looking at your “Refrigerator Defrost and Recovery” graph, it looks like your compressor uses about 110 W of power. Is your compressor rated to draw about 1 A of current? Here’s why I ask…
My girl friend and I recently moved in to a new apartment and were (unpleasantly) surprised by our first energy bill. We apparently used 585 kWh on our first month, which is equivalent to constantly using an average of 813 W of power.
So I went around trying to estimate the power consumption of various appliances and averaging them over a continuous period to compare them our total of 813 W. According to my calculations, here’s what I got for the fridge and my small deep freezer:
First off, the fridge is rated at 691 kWh/year, which is equivalent to 78.8 W of continuous averaged power. But, the compressor says that it uses (up-to) 6.5 A. Multiplying that by 115 V gives me 748 W of peak power. I used a noise meter app on my tablet to listen to the fridge for a few hours (at a 5 sec sampling rate) while no-one was home and found that over six complete cycles, the compressor was on for about 13 minutes every 35 minutes. More precisely, the compressor was on 38.1 % of the time (/pm 0.3%), which means that it should use an averaged power of 748 W * 0.381 = 285 W.
285 W would be 3.6 times higher than the rated power consumption for that fridge, and 35% of our total energy bill. The same calculations for the deep freezer give me:
1.2 A * 115 V = 138 W (max)
138 W * 0.311 = 42.9 W (average), which is 6.6 times less than the fridge.
Unfortunately, I don’t know what the deep freezer is rated at.
So, do you think I found the culprit, or is my calculation 285 W a clear over estimate. Does the compressor continuously draw 6.5 A of current or much less? Looking at your graph, yours seem to draw about 1 A of power, which is closer to what my little deep freezer should draw.
I don’t have a direct way of calculating the power consumption of my fridge, but I was wondering if doing a similar type of analysis with your fridge gives you numbers that are similar with what you got from you TED. In other words, is your fridge compressor rated at around 1 A or much more like mine?
Thanks!
First off: you can’t just multiply V and I on AC power, there should be a 1/sqrt (2) in there somewhere to account for the sinusoidal waveform.
Second: buy a cheap power meter that plugs between wall and fridge cable. They cost like 10EUR. With your electricity bill it should pay for itself in about two weeks.
Not true if you’re dealing with RMS values for V and I as is generally the case in situations such as this. What DOES need to be taken into account is the power factor of the load. For a linear load (which an induction motor approximates), this is the cosine of the phase angle between V and I. A sub-unity power factor probably explains much of the discrepancy in the case of the refrigerator compressor.
thanks, somehow I always thought AC grid voltage was specified peak-to-peak, apparently i was wrong…
“I used a noise meter app on my tablet to listen to the fridge for a few hours”
Very clever. That’s definitely a trick to keep in mind.
However, I think your overall problem is that that 6.5 A for peak power will likely not be the running power consumption of the fridge. Most likely it will be the “worst-case” start up current taken by the compressor motor. In normal operation currents approaching that amount will only be taken for a fraction of a second or so as the compressor starts. For the rest of a run, once the motor is turning and the fluid is moving, the current taken should be a lot less.
Geothermal heat pumps anyone? The ground is a great source (and sink) and renewable energy.
On another topic, entropy is not a measure of disorder. It is a measure of order. The disorder theory works for heat transfer at the macro level but not at the micro level. Entropy, like energy, temperature and pressure is a property of a molecule, atom, or particulate matter. The point of maximum order in a system is also the point of maximum entropy and it is at that point where everything in the system stops moving.
What has a major influence on the COP is the temperature difference between the coold and the hot source. Ventilation behind the refrigerator is important because if you let the temperature of the radiator go up, your COP will just get worse. Same thing if you heat your house with a heat pump, the COP will be better in September and October than in January or February. So if you live in the north, I would recommend an extra wood-heater for the very coold days. Furthermore, you won’t get a heat pump working with an electrical generator.
The “miracle” should be put in relation with the fact that the heat pump requires a large “reservoir” from which heat can be pumped. The problem is that the size of the “reservoir” is linked to housing density. The higher it is, the lower its size per head. You see a lot more heat pumps in individual houses with garden than in high rises, but how much entropy is used to travel in and out of these low density settlement ?
The solution can be found in centralising the heat pump operation and distribute cold or hot water through a specific network. Singapore did this recently. http://www.abb.com/cawp/seitp202/b68e72f3ccfe8658c12578f80030a787.aspx (FYI, I don’t work for them)
My measurements of energy loss due to opening the door of the fridge is much more signif than 0.3%. We open ours rarely (kids don’t only the adults and we’re not apt to open it and start to wonder about what to look for).
To estimate the energy loss due to opening the fridge I compared 12 hour periods – “daytime” when we used the fridge vs “night” when we didn’t.
Roughly 2/3 of the energy use was during the “day” and 1/3 at “night”. At the end of the number crunching (using Wh as the day vs night was not always 12 hours) I estimated an additional 7% energy loss due to door opening.
Note that this was with a standard all-fridge model; not the upright freezer which we converted to a fridge. Converted freezers (chest and upright) use aprox 40% of the energy of an Energy Star rated fridge of the same volume. This is partially due to extra insulation but primarily due to a higher delta-T in the refigeration cycle although I’ve yet to quantify that by measuring the temperature of the refigeration coils.
Note that an all-fridge + chest freezer will typically use less energy than a standard fridge-freezer combo and auto-defrost fridges are the worst of all world – complex control systems and lowest efficiency.
Tom, I’d be interested in your opinion on the more extensive use of thermosiphons / heat pipes / passive heat exchangers. In Canada they are located in communities that depend on permafrost for structural support. They use convection and a phase-change medium. With no energy input, they pump enough heat out of the ground all winter so that it stays frozen all summer.
My thought is that these could be a completely free source of warm air in the winter and cool air in the summer, at least easing the load on air conditioners and heaters, using the ground or a ground-temperature reservoir.
In Toronto the average temperature is probably around 40F. In winter it is likely around 15 degrees, in summer around 75 plus many severely cold and hot days.
A picture: http://www.flickr.com/photos/akfirebug/3502343568/
“Cooling applications have little choice but to use heat pumps, as cooling inevitably involves getting rid of (moving; pumping) thermal energy. ”
Actually there are smarter ways to cooling. At least when it comes to buildings.
If a building has enough thermal mass and insulation, it may well be enough to just circulate cooler outside air during the night in most climates.
Alternatively it is possible to use a ground source directly for cooling. This is especially true when that same source is used for heating during the winter season. If a ground source is used for both heating via a heat-pump during winter and passive cooling during the summer than they’ll help regenerate each other.
I know it’s very common application here in the Netherlands. Almost all new large buildings apply this technique. Simply because it’s the most economical thing to do.
Wonderful article. Heat Pumps are certainly not well understood, and your analysis goes a long way toward correcting widespread confusion in the press and elsewhere. I have two engineering/product development comments:
1. Commercial refrigeration, as used for example in a large convenience store, places the compressors/condensers outdoors in the “hot” bath, alongside the compressors/condensers for the AC system. This solves the need to remove the excess heat generated by the display refrigeration cases when the store is being cooled by the heat pump.
2. At least one German manufacturer of domestic refrigerators makes a very efficient (and very expensive) refrigerator/freezer that uses two variable speed compressors that completely eliminate all of the issues associated with cycling a constant-speed compressor. But, alas, it is not designed so that the variable-speed compressors/condensers can be placed outdoors.