In this post, we’ll put a physical, comprehendible scale on the amount of energy typical Americans have used in their lifetimes. No judgment: just the numbers.
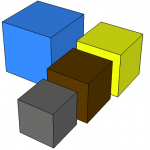The task is to estimate our personal energy volume, so that we can mentally picture cubic tanks or bins corresponding to all the oil, coal, natural gas, etc. we have used in our lives—perhaps plunked down in our backyards to bring the idea home. Go ahead and try to guess/picture how big each cube is.
The resulting analysis is more mathy/quantitative than most of my posts, which might not make for the smoothest reading. Don’t let the math bog you down: the details are there if you want them—but if you just want the answers, they are not too hard to find.
Overall Scale
Okay, we can capture almost the entire story of energy use if we consider oil, natural gas, coal, nuclear fission, and hydroelectric. These take up approximately 40%, 23%, 22%, 7%, and 7% of our total energy diet. We have to correct the hydro and nuclear numbers because the 7% figures are adjusted to put their electricity contribution on the same (thermal) footing as the raw inputs from fossil fuels. The electricity that each contributes amounts to about 3% of the total energy pie. (The fossil fuels are counted by thermal energy input, but hydro and nuclear are more easily tabulated by electrical output.)
Let’s set the scale and talk units. The global power budget is about 12 terawatts (TW), one-quarter of which is contributed by the U.S. It is useful to know that one Watt is a Joule per second, and it takes 1055 J to make a Btu, and 4184 J to make a kilocalorie (food Calorie; see the page on useful energy relations for more on units of energy/power).
The U.S. share, 3 TW, divided by 300 million people, turns into 10,000 W per person. Let’s be clear about the meaning this number. It’s not 10,000 Watts per day, per year, or per any time. A Watt is already a rate of energy use, like a speedometer—easily confused with a kWh of energy. The average American is responsible for 10 kW of continuous 24/7 energy consumption. Think about this: 10 kW of thermal power is equivalent to the heat generated by one-hundred 100 W incandescent light bulbs; seven space heaters; or five full-blast hair driers—operating around the clock for each person (though at 35% efficiency, a power plant consuming fuel at a rate of 10 kW would only produce enough electricity to run 35 bulbs, etc.).
You may object: certainly you are not so energy intensive, based on what you see in your own house. But only 22% of energy in the U.S. is consumed in peoples’ homes. The rest is in manufacture, food production, transportation of goods, service industries, etc. Since you presumably partake of these goods and services in a typical way, you’re stuck with responsibility for 10,000 W of power.
10 kW. Such a nice round number! We can therefore quickly say that a typical American uses energy from oil at a rate of 4 kW, natural gas at 2.3 kW, coal at 2.2 kW, 300 W of nuclear, and 300 W of hydroelectric power. In a bit, we will find it convenient to convert to kilocalories (kcal). So 1 W of power run for a year totals 31 MJ, or 7,500 kcal.
The Fossil Fuels
First, we’ll tackle the fossil fuels. The chemical energy in fossil fuels is not very different from that in the food we eat. Natural gas has 13 kilocalories per gram, oil/gasoline has about 10 kcal/g, and coal typically ranges from 4–7 kcal/g, depending on grade. We’ll use 6 kcal/g for coal.
Oil
Putting numbers together, we see that 4 kW of oil—run for a year—requires 30 million kcal, which amounts to 3 million grams, or 3,000 kg. Three metric tons of oil each year per person! At 135 kg per barrel, this is 22 barrels per year. Does this make sense? The U.S. consumes about 20 million barrels of oil per day, so that each of us uses 24 barrels per year—close enough for a sanity check!
In my lifetime of about 40 years (the brilliance of estimation is that 40 can be “good enough” for a number of years!), I am responsible for the consumption of 120 metric tons of oil. How big of a box do I need? Water requires a cubic meter per metric ton, and oil is about 85% the density of water. So I need 140 cubic meters. The cube root of 140 is about 5.4 meters. So I need a box about 17 feet cubed! That’s going to be an eyesore in my back yard!
Coal
For coal, the numbers work out to 17 million kcal per year, or about 2.8 million grams (much like oil!). At an average of 1.2 times the density of water, 40 years amounts to 92 cubic meters, which corresponds to a box 4.5 m, or 15 feet on a side. Not too different from oil. Note that we get much less of our energy from coal than from oil, but the energy density is much lower, so that the volumes are comparable.
Natural Gas
Our 2.3 kW of natural gas, like coal, requires 17 million kcal, or 1.3 million grams per year. You might remember from chemistry classes that gas at standard temperature and pressure (0°C and 1 atm) occupies 22.4 liters per mole. Methane is CH4, with a molecular weight of 16 g/mol. Our annual 1.3 million grams is therefore 83 thousand moles and occupies 1.9 million liters, or 1900 cubic meters. Over 40 years, this becomes 76000 m³ The corresponding cube is 42 meters (140 feet) on a side. This would certainly catch the whole neighborhood’s attention. And you’ll need one for each member of the household (sized according to age).
If we forgot that this is just a visualization exercise, we might agitate for compressing the gas, as anyone in their right minds would do for storage purposes. In this case, at 190 atmospheres of pressure (a practical limit for steel tanks), the volume is reduced to 400 cubic meters, or 7.4 m (24 ft) on a side. Note the trick of using 190 atm instead of a round 200. Made the math easy, and we’re totally allowed to do such things while we’re estimating (not engineering).
Hydroelectric
What is a relevant volume for the hydroelectric energy you’ve consumed? How about the volume of water that has moved through a dam to produce that energy. Here, the story is simple gravitational potential energy, converted to electrical output at an efficiency of about 90%. The gravitational potential energy of a cubic meter of water is its mass times gravitational acceleration times the height of the water behind the dam. A cubic meter of water has a mass of 1000 kg, turning into 10,000 N of weight when multiplied by g=10 m/s². What is a typical height for a hydroelectric dam? I’ll guess 50 m.
So each cubic meter of water delivers 450,000 J of energy, incorporating the dam efficiency. At a rate of 300 W (300 J/s), this cubic meter provides power for about 1500 seconds (25 minutes). For reference, this water rate corresponds to 15,000 gallons per day—over five-hundred times my household water demand. In 40 years, I need a whopping 850,000 cubic meters of water to flow through a dam somewhere on my behalf. Now we have a cube 95 meters on a side. I have no idea where I’m going to put it! This is a small lake’s worth of water (keep in mind that lakes tend to be much flatter than cubes). Okay, in California, this would be called a small lake, not a large pond, as may be the case elsewhere.
Nuclear
This one is less straightforward than the preceding ones. Each fissioning uranium nucleus releases about 200 MeV (million electron-volts) of energy. This computes to 30 picojoules per fission event (3×10−11 J), so that we need 10 trillion fissions per second to supply our 300 Watt allocation of nuclear power. But we’ve jumped the gun a bit. The fission event creates heat, and this thermal energy is converted into electricity in a heat engine achieving 40% efficiency. So we really need to make 25 trillion fission events per second per person in the U.S.
Our fission reactors use the 235U isotope of uranium, which only comprises 0.7% of the natural uranium mined in the world. The other 99.3% is 238U, which indirectly contributes some fission power by first absorbing neutrons and converting to plutonium within the reactor. Ignoring this sub-dominant channel, we need to mine 140 uranium atoms for each one that goes pop.
So we need to mine 3.5 quadrillion (7×1015) uranium atoms per second per person. Over 40 years, this turns into 4×1024 uranium atoms. Sounds like a lot! Uranium is most commonly found in the oxide form U3O8, which has the tasty name “yellowcake.” To get 4×1024 atoms of uranium, we need 1.4×1024 molecules of yellowcake, which is a mere 2.3 moles. At 842 grams per mole, that makes about 2 kg of yellowcake. Not so bad, after all.
As for volume, yellowcake is 9 times more dense than water, and 2 kg of water would occupy 2 liters. So our handful of yellowcake is 0.2 liters, or three quarters of a cup, or a cube about 6 cm (2.4 in) on a side—about like an American softball. Put it in your pocket! On second thought, don’t.
An alternate take, though not a “fair” comparison: uranium has an average abundance of 2.7 parts per million by mass in the Earth’s crust. So to get the requisite mass of uranium atoms (1.6 kg), we need just over a half-million kilograms of rock. At a density of about 3000 kg/m³, this means about 200 cubic meters of rock, or about 6 meters on a side. This is amazingly close to our fossil fuel volumes! Of course, uranium mining doesn’t work this way: we go for the concentrations, and any random piece of surface rock is likely to fall far short of the average crustal concentration (so don’t try this in your backyard!).
Personalizing the Numbers
I used 40 years for these figures. You can scale volumes (but not cube edge lengths!) by the ratio of your age to 40 years. You may also wish to account for the fact that energy consumption in the past was not as high as today’s numbers we used for the analysis.
But these wrinkles will not change the story very much. And since the exercise is one of visualization, precision is of no consequence.
Picturing the Impact
We’ve worked out all the numbers. Let’s put it into pictures to get a more visceral feel for what the numbers mean. I use a typical San Diego house and yard (2000 ft², and 7200 ft², respectively) for comparison. Note these cubes apply to just me. My wife requires another set (but I’ve run out of room in the backyard!).
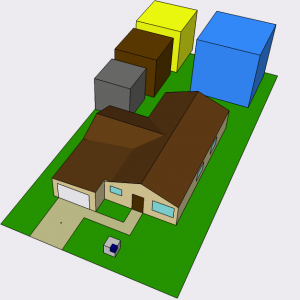
Fitting the coal (gray), oil (brown), compressed gas (blue) and crust with enough uranium (yellow) to power my American 10,000 Watts for 40 years. The actual softball-sized uranium yellowcake needed is in the middle of the driveway. The cube in the front yard will be explained later.
The cubes are color coded: dark brown for crude oil, gray for coal, blue for compressed natural gas, and yellow for the amount of average crustal material containing the requisite amount of uranium (though the actual uranium fits in your pocket). Each of these cubes corresponds to 40 person-years of typical usage. Add up the person-years in your house to figure out how to scale these volumes.
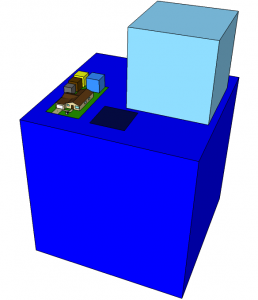
Same as before, but now including the uncompressed natural gas (light blue), hydroelectric water volume (dark blue), and the size of a photovoltaic panel (blue-black) that could replace all cubes (the necessary materials are in the front yard).
Panning out, we see the scene set on top of the appropriate-sized cube of water (deep blue) for hydroelectric production. This is a big volume for only 3% of the energy. But it is replenished, and so is not a good direct comparison to the other resources (we could compare the volume of dam needed, or note that the daily water use is about the size of the yellow cube). We also now see the volume of natural gas in uncompressed form as the light blue cube. This is the appropriate volume of gas as burned at the stove-top, furnace, or water heater.
Also shown for reference is the size a 15% efficient photovoltaic (PV) array would have to be to supply the entire 10,000 W average power an American demands today. The 18×18 m array produces 48 kW in full sun, but I’m only counting on an average of five hours of full-sun equivalent each day (San Diego is closer to 6, actually). Note that the PV array will last approximately the same 40 year timescale, and is thin enough to require far fewer materials than the other streams—even considering eventual replacement. Sitting in the front yard is the amount of material volume needed to construct the 4000 kg of panels, coming out to a cube 1.15 m on a side. The actual high purity silicon is a cube 0.5 m on a side, seen as a dark blue inset in the solar materials cube.
Not shown are the resources needed to make the PV panels. With an energy return on energy invested around 10:1 (takes about 3 years-worth of the panel’s energy output to make each one; lasts at least 30 years), we could either increase the array area by 10% to cover a PV-supplied energy chain, or use our conventional boxes at one tenth the volume shown.
Price Tags
The installed solar array would cost approximately $200,000 (no storage). Meanwhile, the cube of oil, at $100/bbl would cost $88,000, and the coal and natural gas—if used to produce electricity at 35% efficiency and $0.05/kWh—would cost about $40,000 each (over twice this in California), for a total outlay of at least $170,000. Same ballpark, actually. If I instead use gas for cooking and heating, I would pay $26,000 rather than $40,000 for the gas at $1 per Therm (100 ft³ = 2.8 m³ contains 1.02 Therms of energy).
Yes, I used today’s prices and not the average prices over the last 40 years. But the comparison between fossil fuels and solar, for instance, is of interest for the future and not the past. Anyone want to guess whether the fossil fuel prices over the next 40 years will go up or down?
What of It?
The results of this exercise are intended to do little more than put a visual scale on the materials involved in the energy requirements of a typical American citizen. Some may be amazed at how large the volumes are, while others may be amazed by how small. They are what they are, and we can carry these visualizations around in our heads for whatever purpose.
Personally, I am impressed by the relative similarity of many of the block sizes. I don’t find any of them to be mind-blowingly monstrous, but at the same time I am humbled by the invisible (to me) impact these cubes represent in our wider world. I am impressed by the compactness (especially in comparative volume) of the solar array that accomplishes the same energy yield over 40 years—although it is not my intention to trivialize the practical challenges of transitioning to a fully solar energy system, or to suggest that a fully solar system is the appropriate approach. Nonetheless, solar energy is often characterized as pathetically diffuse and expensive. But when multiplied by decades of sun, the materials and volume required are rather advantageous, and the cost comparison is not frightening.
Views: 1381
The hydro vs solar comparison is really unfair. In one case you count the volume of water that has to flow through, while in the other you count the size of the solar cell. Instead you should either count the size of a personal dam, or the volume of photons incident on the solar cell in 40 years (which I work out to a cube about 5000km on a side, which luckily isn’t supplied from the Earth)
Actually, I think it would be fair to figure embodied energy of the dam itself as compared to the PV panels. Additionally, solar radiation isn’t typically figured as a finite, non-renewable resource; water, on the other hand really is, given that less than 1% of the total volume on the planet is potable.
Since Tom is starting with total energy at 12 TW, the embodied energy is figured into the solar panels, depending on the year of manufacture. The hydro, however, was typically built a long time ago, and the energy has been long since dissipated into entropy, or is still in the process of doing so.
Interesting point about the photon cube size!
I agree that the hydro example doesn’t really compare well, but I think the solar panel comparison to fossil fuels makes sense, in a way.
I’d also be curious to see the volume of waste product produced by each (carbon dioxide and ash/particulates for fossil fuels, nuclear waste + volume of containment vessel to store long-term). Is there any waste produced by hydroelectric? Silt, I guess?
Wow, solar is looking great! Especially considering your prior posts (lets try not to cook ourselves) and the direction fossil fuel costs are sure to move in the future.
Interesting, as always!
An important point about the total energy picture is that not all forms of energy are created equal. That is, the current state of our technology does not allow for the easy conversion of sunlight into liquid fuels for transportation purposes. We are near totally dependent on petroleum for that, despite the current hype over PHEVs. Until such time as we are willing to greatly reduce this dependency, there is no readily available, scalable, and affordable alternative to oil.
Also, it bears repeating that nationally, our electricity is mostly generated from coal and natural gas.
Thanks for the very cool graphics Tom! Nothing quite like a hotel of energy next to your house for comparison.
“That is, the current state of our technology does not allow for the easy conversion of sunlight into liquid fuels for transportation purposes.”
Depends. Synthesis of hydrocarbons from carbon feedstock like coal is a commercial process (SASOL). Synthesis from CO2 or biomass may not be, but my impression is that the chemical processes are fairly well understood. Less a matter of technological know-how and more of infrastructure, because no one outside of wartime Germany or apartheid Africa had much incentive to work on alternatives to sucking oil and gas out of the ground.
I’ve never been able to find a good price or conversion efficiency for synfuel, but I have a vague impression it’s comparable to current prices.
OTOH, assuming 30% efficiencies, solar electricity -> fuel -> car motion is about 1/9 the efficiency of solar -> electric car or train, and to be avoided. And 30% is optimistic for the car burning fuel; no idea about the synthesis side, it just seems a conservative bet for industrial processes.
There are a number of companies out there working on CO2-> gasification processes, among them a company rather arrogantly named “Green Freedom.” The problem of course is that it requires a lot of energy (the Green Freedom start up plant comes with a fission reactor to power it), and is very vulnerable to swings in the gas price. I think that it could be made competitive with current fossil fuel prices, but the big block is the tremendous start up costs you’d see in it.
Tom,
I agree with other commentators regarding resources required to access solar energy. By representing it as an area rather than a volume, you seem to indicate that solar requires no resources at all. Edward Tufte strongly suggests not mixing number of dimensions used to depict the same units in the same drawing.
Questions: What did you use for your estimate of crust required to produce the nuclear electricity? Is this crust uranium ore of a quality mined during your lifetime? The text suggests that crust is a random chunk, which would be grossly unfair to nuclear, since conventional fossil fuels were not treated in this manner.
Also confusing was your treatment of thermal versus electrical energy. Powerplant engineers typically use subscript (e) or (th) to differentiate. About 10 kW(th) is burning in this country for each of us, which is not the same as 10 kW of electrical power. (unless one is really wasteful and wants to burn about 30 kW instead!) Representing thermal power with lightbulbs muddles the issue.
Your postings on TOD have been interesting and thought provoking in the big-picture sense, and I look forward to reading more.
What—you can’t see the thickness of the solar panel in the drawing? Trust me, there is volume there! All kidding aside, the panel is certainly thin, requiring a volume of material that is small compared to the other boxes. Even at an average material thickness of 1 cm (grossly thicker than needs to be), we’re talking about 3 cubic meters of stuff.
The more even-handed treatment of nuclear leads in the text: a softball of yellowcake. Doesn’t show up on the graphic, and I found it curiously interesting that using average crustal abundance produces a similar-sized cube to the fossil fuels. Not intended to be an unfair comparison.
You are correct that 10 is a thermal number, not electric. I will clarify in the text.
Three cubic meters would show up nicely as a cube in front of that white garage. However, the silicon used in solar cells is highly refined, and a fair comparison would include all material dug up for your cells, the batteries (since other forms are already stored energy), and structural support. It ought not include power inverters and copper since transmission and distribution equipment was neglected for the other sources.
The curiously interesting, oversized yellow cube reflects the energy density difference inherent in chemical versus nuclear processes. I still maintain that by randomly digging up crust, you are going out of your way to make nuclear look bad. It is easier to make nuclear look better, since the spent fuel could be reprocessed or eventually even used in breeder or hybrid fission-fusion reactors.
Perhaps a fair comparison for energy density of hydro would be the volume occupied by the dam and its contents, divided by the total energy yielded over the lifetime of the dam.
It was not my intention to be unfair to nuclear: I will add the softball to the figure when I get the chance, and also the solar panel material cube (but not all the dug up material, as only nuclear received that particular treatment). There have also been lots of good points about how to fairly represent hydro, which I will consider. The simplest remedy for this is to clarify that the hydro is not an apples-to-apples comparison.
“Uranium ores in the United States typically range from about 0.05 to 0.3% uranium oxide (U3O8).”
http://en.wikipedia.org/wiki/Nuclear_fuel_cycle
So, to get from yellowcake back to ore requires a factor of about 1000, and your dug up stuff for nuclear fuel becomes a cube ten softballs on a side. Energy requirements for enrichment are small compared to energy yield from nuclear fuel.
Coal, gas and oil are combustible in their native form, so do not require this sort of special treatment. However, the waste volume of CO2 from all of this combustion might be represented by a very large black cloud at standard temperature and pressure above the whole house.
I think in order for solar to be compared fairly you would have to show, for instance, the amount of earth mined to acquire enough quartz/silicone/what-have-you for the panels themselves. This is basically what you did with nuclear in your post, and I think not treating solar in the same way is a tad misleading. Additionally, you don’t address the materials or space required to store the energy generated from the panels when the sun is not shining. As one of your other posts discussed, this requires a fairly substantial battery array.
That said, it’s certainly an interesting way to look at our energy consumption. Please keep this posts coming – as an engineer I really enjoy the numbers-based approach you take to discussing problems.
Silicon (note: no ‘e’) is over 1/4 of the mass of the earth’s crust, or approximately 100,000x more common than uranium. So, in comparison with the uranium cube, 3 cubic meters of silicon would necessitate the “mining” (a curiously strong word to use for scooping up sand…) 12 cubic meters of crust, or a cube about 2.3 meters on a side.
heh, thanks for catching that misspelling. The silicon was just an example – there are other materials, such as copper, and in some cells, some heavy metals that would require quite a bit more mining.
To clarify regarding hydro, water volume could be maximum static volume, instead of total integrated flow. Maximum static hydroelectric volume represents an ecological footprint in a manner similar to that obtained by measuring the volume of a mountain burned as coal. We can’t enjoy the valley or the mountain if we want the Joules.
Now, if you were take the next step, you would need to create one or possibly two related visualizations. The first one would be the presistent wastes generated by the various methods. For example, we would need cubes showing how much airborne, water and ground pollution was generated for each amerikan, and each source. Of course, the earth can (in some cases) absorb some of the pollutants generated, so there would be some offsetting, but most of them persist in the enviroment well beyond 40 years. Hyrdro would come out looking the best, while the FF and nuclear waste cubes would be simply awful. Since Pollution from gas and coal often combines with elements allready present in the atmosphere, these ‘waste’ cubes(I would think) would actually be somewhat larger than the consumption cubes. I think that would be a interesting tie-in. A cube could show how much volume of air is polluted, how many cubic miles of water poisoned and made useless for any other purpose, ground contaminated and so on.
Another(possible) breakdown would be how each ‘consumer’ in the US actually utilized that energy. Of course, we would find out long before anyone ran the actual numbers that the vast majority of that energy went to shuffling amerikans around in 2 ton steel and glass boxes on vast ‘freeway’ systems that themselves would also consume a huge amout of the ‘cubes’ just to maintain. The purpose of all that movment would mostly involve ‘shopping’ and driveing 60 miles a day to get to work. I think that too would be an interesting visualization. You could say, that slice went to ‘defence'(garrisoning the planet), that slice went the criminally wasteful industrial ‘food’ system, that slice went to air-travel and so on. That would probably be better shown as a national cube rather than individual like in your yard, but then again, saying this is what you pay to keep suburbia, jet travel and the worlds most useless and expensive military running wouldnt be bad either.
As to the comment about the cubes not seeming all that big, once you multiply and stack those cubes by 300 million ‘consumers’ they would get large in a real hurry.
Roughly speaking, the U.S. consumes 25% of the world’s share of energy. So the world has the equivalent of 1.2 billion American energy consumers. The cube root of this is pretty nearly 1000, so we could simply replace meters with kilometers in all cube dimensions. Big to us; small compared to the Earth—emphasizing how rare and precious the fossil fuel resource is on the Earth scale.
You left out human food consumption. That is very roughly about 4,000 kCal per day (that includes spoilage etc.). There are 4.2 kJ per kCal, so this is 16.8 MJ/day, or 6136 MJ/y. Photosynthesis is less than 1% efficient at producing stored carbohydrates, proteins and oils, so one needs at least 614 GJ/y of insolation to create those calories for a vegetarian diet. Multiply by a factor of 10-20 for meat diet. In Iowa insolation is about 6 kWh/m^2/day, so you need at least 78 m^2 of crop area for vegetarians, about 2000 m^2 for a meat-oriented diet. All the energy required by the farmer (fertilizer, diesel) and transportation is presumably already included in your other cubes.
When replacing oil with electricity, the PV required is much smaller than your numbers suggest, because electric vehicles are more efficient than internal combustion engines. PV produces power that is directly usable at efficiencies around 90%; oil produces heat energy that is subject to the Carnot limit in efficiency. Thus it takes less PV to power EVs. For example, it takes about 3 kW of PV in San Francisco to power a Nissan Leaf 15,000 miles a year. SunPower’s 230 W modules are supposedly 18.5% efficient, and take 1.244 m^2 of roof area. So 3 kW is 16.2 m^2, or 175 ft^2.
I agree with the other comments that the comparison to the solar panels is grossly misleading. The active ingredient in PV panels is 99.99 percent pure polysilicon, produced by much the same ultra high-tech fabrication process as computer chips. Not energy or resource neutral by any stretch of the imagination.
The comparison to a cubic meter of “material” needed for the PV panels essentially implies that you can scatter a cubic meter of sand on your lawn and get decades of high quality electrical energy from it.
Not even close, and a great disservice to your readers to present such a misleading point of view.
The key characteristic here is energy return on energy invested. It takes about 3 years-worth of a panel’s energy to fabricate the panel out of the sand and other materials. If the panel lasts 30 years, you get 10 units of energy out of every one unit put into its manufacture. So you could represent the manufacturing inputs by reducing all conventional cube volumes by a factor of ten, or by expanding the array size by about 10% to provide the extra energy needed to replace the energy investment. I agree that the energy input is crucial to consider, and that sprinkling sand on the yard is not the way to go (nor would it help to distribute any of the cubes on your yard in this way). But solar is still energy viable and useful.
The visualizations in the post put imaginable sizes on things, but does not assert that the materials corresponding to the panel reflect a 1:1 replacement for the fossil cubes. I put the solar materials cube in after one reader complained that the area represented by the panel did not allow volumetric comparison. Just trying to please…