 Ever wonder how efficient it is to heat water? Of course you have! Ever measured it? Whoa, mister, now you’ve gone too far!
Ever wonder how efficient it is to heat water? Of course you have! Ever measured it? Whoa, mister, now you’ve gone too far!
I recently devised a laser-phototransistor gauge to monitor my natural gas meter dial—like ya do. As a side benefit, I acquired good data on how much energy goes into various domestic uses of natural gas. Using this, I was able to figure out how much energy it takes to heat water on the stove, cook something in the oven, or heat water for a shower. Together with the knowledge of the heat capacity of water, I can compute heating efficiency from my measurements. What could be more fun? I’ll share the results here, some of which surprised me.
Heating Basics
The amount of energy it takes to heat water is so well-established, that it is the basis for several prominent units of energy. For instance, the calorie is the amount of energy it takes to heat one gram (1 mℓ) of water by 1°C. As a straightforward extension, 1 kcal = 4184 J (often Calorie with capital C) is how much energy it takes to heat one kilogram (or liter) of water by 1°C. Likewise, 1 Btu = 1055 J is the amount of energy it takes to heat one pound of water by 1°F.
So if I want to take 500 mℓ of water from 18°C to boiling, I need to expend 82×0.5 kcal to get the job done, or 171.6 kJ.
Measuring the Gas
My natural gas meter usually receives little attention from me—which is saying something for a person as measurement/data crazed as myself. The reason is that the meter does not provide sufficient information to track small expenditures without vigilant monitoring. As explained in the pilot lights post, there are dials that make revolutions once every half-cubic-foot and two-cubic-feet, then a jump to 1000 cubic feet. The jump is so large that one cannot walk up to the meter and know at a glance how many wraps the high-resolution dials have made since the last look.
Rather than parking myself outside for days on end to keep track of my gas gauge, I bought a cat-toy laser pointer and modified it to be powered by a constant 5-volt power supply. I aimed the laser at the ½-cf dial so that the black needle would interrupt the beam once per revolution. Then I set up a photo-transistor to “watch” the laser spot, and tuned the sensitivity so that the needle would make a robust change in the photocurrent. The laser and detector were shoved into a crudely drilled block of plywood to point at the same spot on the dial face, and then clamped to the meter. A dishtowel provided ambient light baffling, and a plastic shopping bag gave it some modest protection from rain and a certain trashy look. Thankfully, our gas meter information is now digitally transmitted. I can’t think what the meter reader’s reaction would be to walk up on this clap-trap arrangement (glowing red at night, no less).

Contraption attached to gas meter. A red glow can be seen from the laser. The green/black wires go to the phototrnasistor.

Close-up showing the laser spot illuminating the half-cubic-foot dial, ready to sense the passage of the dark needle. See also a picture of the same meter face-on in the pilot light post.
I kept the electronics in the garage (only the laser and sensor were outside), accompanied by a data acquisition unit and a computer to log the continuously sampled series (3 second samples were sufficient). Not the most elegant way to get the data, but I used stuff I had on hand. And it worked. And the plots are nice.
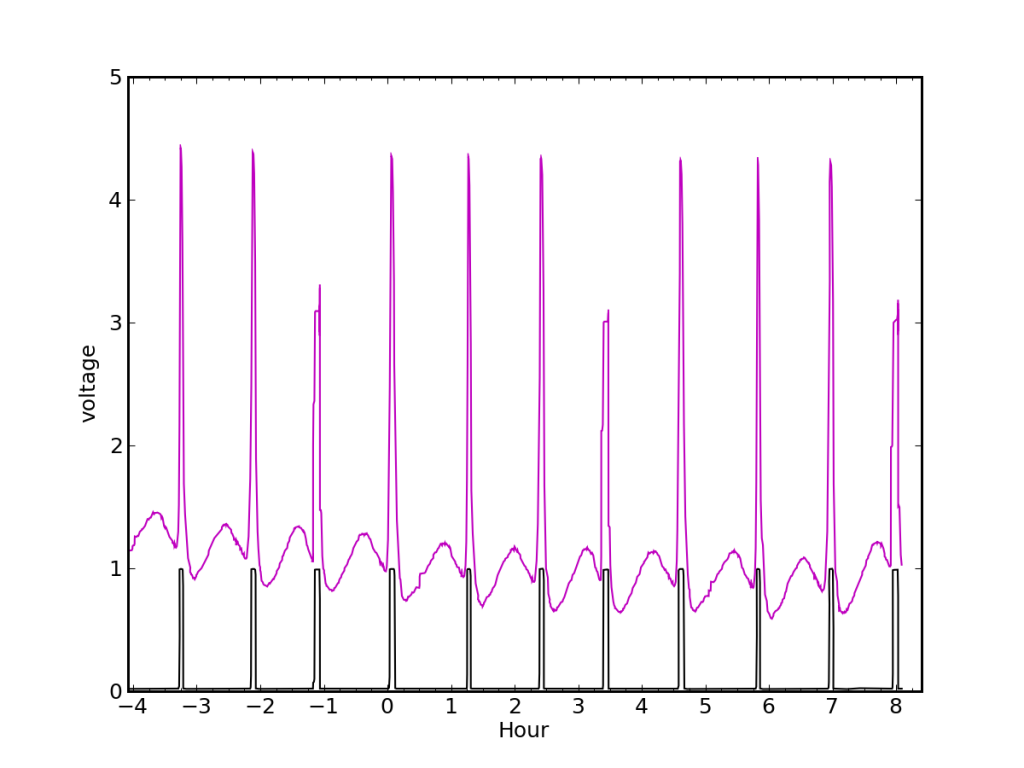
Here we see the hot water heater pilot light causing the sensing circuit to respond in a periodic fashion. Every time the needle crosses in front of the laser, the sensor voltage goes way up. The needle can be a little jerky, so it sticks and slips—causing some spikes to be stunted and steppy. In this plot, ten revolutions span 11.2 hours. At 510 Btu per revolution, this corresponds to 133 W of continuous power in the pilot.
Most of the time, the water heater pilot light creates our only gas demand. In the summertime, even our shower activity—albeit modest—is satisfied by the pilot. We can see in the plot above the periodic signature of the needle interrupting the laser, and also a sinusoidal behavior between needle crossings. Unintentionally, the sinusoid gives a useful cue as to exactly when a high-flow demand (stove, oven, heater) is initiated, so that one does not have to wait until the needle event for the first indication. The sinusoidal pattern is presumably from scattered light off of irregularities in the needle hub.
Even without the extra benefit from the hub, one can determine how much gas was used by noting how many cycles appear between the languid pilot spikes, compared to how many revolutions the pilot would have produced in the same period.
Each half-cubic-foot of gas is equivalent to 510 Btu, since 100 cubic feet delivers 1.02 Therms, and a Therm is 100,000 Btu. Therefore, each turn amounts to 538 kJ, or 0.149 kWh.
Stove-top Boil
Enough with the preliminaries. I lured you in with promises of efficiency measurements, and went off instead into some mad scientist tangent.
If I place 500 mℓ of water in a copper-bottomed 4-quart (approx. 4 ℓ) pot, and set this pot—without lid—on top of the largest burner and let-er rip, what efficiency do I get? The flames are mostly hitting the bottom of the pot, but maybe a smidgeon of curling around the sides. Any guesses?

Two languid pilot light needle sweeps frame this series. Shortly after the first pilot spike, the gas stove was turned on, producing two quick spikes and a sped-up periodic signature in the baseline. It is 65.3 minutes between pilot spikes, during which time the needle made three turns. Ordinarily, it would take 67 minutes between pilot spikes (one turn). We can therefore attribute 2.03 turns to the gas stove, amounting to 1033 Btu, or 1.09 MJ. The 1.95 minutes between stove spikes translates to a burn rate of 15,700 Btu/hr, about 460 of which are from the pilot light.
Starting from an ambient temperature of 18°C (water at equilibrium), and heating to a boil, the gas meter reveals 1.09 MJ of energy was used on top of the steady burn from the hot water heater pilot light, at a rate of 4500 W (about 15,000 Btu/hr). Meanwhile, it was supposed to take only 171.5 kJ of energy to boil this amount of water. So the efficiency was a mere 16%.
I was surprised. Are you surprised? I mean, burning the fuel is itself highly efficient. The pot sits right atop the flame. Dirt simple. Some heat escapes around the side, some goes to heating the pot itself, but come-on—16%?!
In another test on another night, I boiled 500 mℓ of water starting at 16.5°C on a smaller burner (1670 W, or 5,700 Btu/hr). I used the same pot, but this time with its lid. I put the burner on full power, but its smaller diameter meant that no flames visibly licked around the bottom of the pot. Want to guess as to the efficiency in this mode? I deem this mode to be about as efficient as I am likely to get on the stove-top using standard practices. The answer: I used 640 kJ of gas for something that should have taken 175 kJ for an efficiency of 27%. An enclosed kettle on the same burner delivered the same result.
Okay, so a 68% improvement over the full-throttle approach is a significant gain (although it took almost twice as long). But still, I was surprised that I top out at less than 30% on a gas stove burner.
Incidentally, from the rate of cooling after the burner was turned off, I gather that the water remaining in the open pot lost heat at a rate of about 300 W through convection, radiation, and possibly some conduction to the grate. These mechanisms are roughly proportional to ΔT between the water and the environment, so on average come to about 150 W during the linear ramp-up of temperature from ambient to boiling. This would have cost 63 kJ in the slow case (about 10% of the total), or about 35 kJ in the full-blast case (3% of the total). But the lidded case would actually lose heat less quickly than these numbers indicate, as the loss rate is based on an open pot after the boiling test was complete. In either case, loss from the pot to the environment appears to play a relatively minor role.
How About Microwaves?
Okay, the stove top delivered disappointing efficiency results. But right above the stove, I have a microwave. Naively, I expected the microwave to be something like 80% efficient at delivering energy to the water. The thinking goes like this: the interior of the microwave oven is a good reflector for microwaves, so they rattle around until they find an absorber; namely, the food/water. Of course there will be some loss in generation at the magnetron tube (I imagine it gets hot). And the walls may not be perfect reflectors, so that after twenty bounces, there may not be much energy left. But still, 80%—right?
This time, I put 500 mℓ of 18°C water into a plastic measuring cup (63 g) and heated on full power for 90 seconds, measuring the temperature afterwards. The water reached 50°C, demanding 67 kJ of energy. Meanwhile, both a Kill-A-Watt and TED (The Energy Detective) told me that I used 157 kJ of utility energy. That’s 43%, folks. Yes, I’m disappointed too. A later test at 120 seconds produced 60°C water (this time from 22°C) for a computed 40% efficiency.
Considering that electricity often comes from fossil fuels at 30–40% efficiency, the microwave (as tested by me) is only 15% efficient at transforming fossil fuel heat into heated water. That’s worse than the stove top—especially the slow-and-steady version.
Electric Kettles
What about electric kettles, where a heating element is immersed into the water, directly heating the thing you care about? To boot, these kettles often have insulated sides, keeping the heat where you want it.
I borrowed a kettle from work, and heated 500 mℓ of water from 18°C. I was able to suspend a thermometer in the water in a way that did not compromise the lid or spout. After 152 s, the water was making plenty of happy bubbling noise and the thermometer read 100°C—although apparently it was not as well-calibrated as I would have expected, since it sailed up to 105°C after 173 s. The water was obviously in a vigorous boil by then, and I shut the kettle off at 210 s (I should have let it turn off on its own, but lost patience with its inefficient lethargy).
Both the Kill-A-Watt and TED agreed that the kettle consumed about 1440 W. So while I needed 0.5×4184×82 = 171.5 kJ to raise the water to boiling from 18°C, I spent 219 kJ by the time the (erroneous) thermometer read 100°C; 249 kJ by the time a full, roiling boil was obvious; and 302 kJ by the time I shut the device off. Using the middle number, I calculate 69% efficiency. I get 78% if I use the shortest time, when I thought I was at boil. But by the time I shut it off, we were down to 57%, and falling. Who knows how far it would have sunk before shutting itself off (kicking myself that I don’t know).
If the shutoff is sufficiently sensitive, it seems electric kettles are capable of something like 70% efficiency or better. It would seem to beat the pants off the other methods—except for two caveats.
The first is the one raised for the microwave. If your electricity comes from fossil fuels, 70% efficiency becomes 25% in turning fossil fuel energy into hot water. The stove top is competitive.
The second caveat is that kettles suffer a sometimes rather large inefficiency due to lax filling practices. A kettle is considered to be a reservoir. Few measure the amount of water they put in. As long as it’s enough, game on. So the tendency is to overfill. All the water gets heated. Only some is used. This practice is probably even more pervasive in communally-shared kettles, and could easily cut a deep hole into the net efficiency. By contrast, microwave practices typically heat exactly as much as is consumed. A kettle with 50% over-fill turning off on its own sweet time can easily sink to the levels achieved by the microwave.
Hot Water Heater
While we’re talking about the efficiency of heating water, how well does my gas-fired hot water heater perform in transferring combustion energy into the water tank? Seems like it should be pretty good: few places for the heat to go except into the water (although the flue does get super-hot).
Practically speaking, efficiency suffers from slow heat loss during idle times, and from loss through the pipe walls during delivery. Tankless applications can avoid these two loss mechanisms. But let’s separate these out and ask only about the direct efficiency with which combustion energy gets into the water in the first place. To do this, I poured hot water into a bathtub until the water heater came on. I let the heater complete its business, then waited about an hour, after which I drew another batch of hot water until the heater activated again. This way, the second heating did not have to compensate for long-term loss of heat from the reservoir.
Mind you, this experiment represented unusually excessive hot water use in our domicile, but I did it for the people. And we did manage to enjoy baths in the bargain.
I measured the temperature of the water emerging from the (hot only) tap, and from a tap right at the inlet from the street (adjacent to water heater, too). I used the water meter by the street to gauge volumetric use to a precision of 0.01 cubic feet (0.3 ℓ). And, of course, the gas meter told me how much energy was consumed.
On the first wave, I used 1.39 ft³, or 39 ℓ, heated from 22°C to 53°C (remind me to turn the heat down; I should also note that the water came out at 50°C on the first draw, but it had cooled in the tank for some unknown time). Multiplying these fine numbers by 4184 J/ℓ/K, I compute an energy demand of 5.1 MJ. Meanwhile, my gas gauge made 17.15 revolutions at 510 Btu/rev for a total of 9.2 MJ. The efficiency computes to 55%.
On the second withdrawal—this time based on a recently heated tank, it took 51 ℓ before the heater engaged, after which the gas dial made 19.15 turns. This time, the demand was 6.6 MJ, while the gas cranked out 10.3 MJ. The efficiency is 64%.
Again, I find myself disappointed. I need to re-adjust my intuition about how straightforward it is to channel heat from a flame into water on the other side of a metal wall.
Bonus Round: Gas Oven
I seriously doubt I’ll get around to another post detailing the things I learned from my laser-gauge gas meter. So I’ll stick in here what I learned about my gas oven. How much energy does it take to “charge” up? How much power to keep steady? How much “on” time equivalent does it take for the pre-heat phase?
I heated my oven to 425°F (218°C) from an ambient 20°C temperature. It took 9.5 minutes to arrive at the setpoint, during which time the half-cf dial on the gas meter made five turns. Correcting for the water heater pilot light rate, this action took 2480 Btu, or 2.6 MJ (0.72 kWh). The burner operated at about 4800 W (16,300 Btu/hr). Thereafter, I found that it took a steady 1500 W to maintain temperature: I left the oven unopened and undisturbed for the better part of an hour to make sure I reached equilibrium—all for the sake of experiment. This means that the preheat phase uses the same amount of energy as 30 minutes of steady operation. You don’t need fancy gauges to tell you this if you note the preheat time is 10 minutes and observe that the burner is on one third of the time during steady operation.
If you’re heating a pizza in the oven that requires ten minutes of cook time, then only 25% of the total energy is spent in cooking mode, the other 75% in preheat. If cooking something for an hour, the preheat surcharge drops to 15%.
Although I am embarrassed to reveal the efficiency of cooking pizza in the oven (since this is not unknown in my household), I owe it to myself to carry out the calculation. Let’s say I heat a 383 g pizza by 200°C (but that it’s heat capacity is in between that of water (at the high end) and more typical materials—say 2000 J/kg/K. So I need to inject 0.383·2000·200 = 153 kJ. Meanwhile, my oven heats up for ten minutes and then the pizza spends ten minutes in the oven. I count 2.6 MJ for preheat, and an additional 0.9 MJ for the cook time. In the end, I manage to get 4.4% of the expended energy into the pizza. If I instead tried 6 minutes of full-power equivalent in the microwave oven (at 1750 W), I might get near 25% efficiency—and a flaccid crust.
Summary Table
Lots of numbers thrown around in this post. Here’s a table of my results.
| Activity | Efficiency | Adjusted Efficiency |
| Boiling water on gas stove, full blast, no lid | 16% | — |
| Boiling water in same pot, smaller burner, with lid | 27% | — |
| Boiling water in kettle on small gas burner | 27% | — |
| Heating water in microwave oven | 43% | 15% |
| Boiling water in electric kettle | 50–80% | 18–28% |
| Hot water heater, including tank loss | 55% | — |
| Hot water heater, without tank loss | 64% | — |
The adjusted efficiency is the fossil fuel equivalent if electricity is derived from fossil resources (coal, natural gas) at 35% efficiency. The range on the electric kettle depends on how quickly the kettle shuts off in response to boiling water.
Testing Without Lasers
If you wanted to replicate or extend these experiments, is it hopeless without the laser-sensor gauge I created? Not at all—although slightly less convenient. In fact, I carried out the hot water heater test after I had already dismantled the gauge. Here’s one trick. Once you’ve characterized the burn rate of various devices (e.g., stove burners on max flame; oven while burner is on; water heater; furnace; etc.) then all you need is a way to measure time when the (audible) burner is on.
As alluded to above, keeping track of the fraction of time the oven burner is on in steady operation is enough to tell you how much energy goes into preheat vs. holding temperature. Even without calibrating a stove burner, different configurations (lid, different pots, etc.) can be compared against each other just by timing.
To measure the rate of gas usage of various devices, make sure that device is the only thing on, and time how long it takes the half-cubic-foot (or 2 cf) dial to make one revolution. Together with knowledge that each half-cf translates to 510 Btu (538 kJ), you’re pretty much set. Having a way to measure volumes and temperatures also came in handy for me.
What of It?
Heating water is less efficient than I originally thought. All the same, it will always take 1 kcal to heat 1 kg of water 1°C, and heating water is something we will always be interested in doing. Yet, efficiencies are middling-enough that we can’t expect gigantic improvements. Heat pumps could break the 100% efficiency barrier (by a factor of several), but these are impractical for small-scale applications.
Should you react to the numbers above by rushing out to buy an electric kettle, with the promise of tripling the efficiency over the stove-top solution? In part, this depends on your source of electricity. If your electricity is derived from fossil fuels, and you otherwise have a gas stove, then it’s probably not worth it. But even if going from an electric stove to en electric kettle, we must consider the embodied energy of the kettle. I discussed two methods for estimating embodied energy in another post, which for this case results in something like 50 kWh of investment. Each cup (250 mℓ) of water takes 0.03 kWh of energy at 70% efficiency. If you’re tripling efficiency, then you save 0.06 kWh per cup, and need to boil over 800 cups before the thing pays for itself, energetically. Maybe this makes sense. But it’s not a burning imperative.
As with many things, a far more effective strategy is to first recognize how and why you use sources of energy. After developing an awareness, you are far less likely to heat excess water in a kettle that you don’t plan to consume. Shorter, less frequent showers can have a far bigger effect on your energy use than how you heat water for tea. It comes back to behaviors.
In the meantime, it’s kind-of nice to have some numbers for water heating efficiencies—as disappointing as the numbers themselves are.
Views: 20257
I’ve often wondered about heat lost at the stovetop. It might be interesting to compare various sorts of electric burners, including induction heating. I suspect they’d all be worse than the ones you’ve written about.
A correction: you do not want to heat your pizza by 200° C. While your oven may be set to that temperature, the pizza won’t get that hot until all the water has been boiled out of it, which means burnt pizza. The energetics of cooking are messy, because you’re trying to increase temperature, evaporate water, *and* do chemical reactions. I suspect the energy that goes into chemistry is negligible, but the energy that goes into evaporating water is huge.
A caveat: the energy-inefficiency of cooking doesn’t matter if it’s cold outside. If you’ve got a gas furnace and a gas stove, all the stove’s heat, both useful and wasted, goes into your house, reducing the demand on your furnace. In fact, it’s probably a net gain, because 100% of your gas stove’s heat goes into the house, while the furnace loses some out the chimney. On the other hand, if you’re using air conditioning, it’s a double whammy. You pay for the heat your stove wastes, and then you pay again to remove that heat from your house.
Caveat to caveat:
Efficiency can still matter even if it’s cold outside if you (like I) choose not to heat your home, or have a well-insulated or passive house. In this case, you might consider the extra heat to be a perk that you’d otherwise not experience. But the amount of energy is very small compared to what the furnace cranks out (stove burner at 5–15 kBtu/hr, compared to furnace at 80; stove burner on much shorter time than furnace during day). Seeing the room go from 14%deg;C to 14.3°C doesn’t register as a bonus.
Not quite true about the water in food limiting the temperature. It depends where the water is in the food and whether it is bonded in some way. Certainly any free water floating on the food will commence boiing but only the food in close contact with the water will be temperature limited. Else, how would you cook a roast ( meat and vegatables) to perfection?
The temperature of the food is subject to the complex pressure gradients and complex chemical bonding within the food.
I always love your exposition of basic figures like this, but this time around I found my inner pedant cringing at the ℓ for litre. Wikipedia says “this usage has no official approval by any international bureau.” [1], while the BIPM only mentions l or L [2]. Also, there should be a space between the number and the unit, even for 218 °C.
On a less pedantic note, I would be very interested in checking stovetop efficiency for an induction hob. I am still surprised at how long things take to heat up on our current gas hob compared to the induction hob I had in our previous home – I’ve taken to heating our pasta water in our electric kettle (which is rated at 2.5 kW) and then transferring to the hob. I suspect the heat loss will be much lower on induction as there is no high temperature element to radiate away that heat, and little convection losses.
[1] http://en.wikipedia.org/wiki/Litre#Symbol
[2] http://www1.bipm.org/jsp/en/ViewCGPMResolution.jsp?CGPM=16&RES=6
[3] http://www.bipm.org/en/si/si_brochure/chapter5/5-3-2.html
Pedantry which Ieads to confusion is no virtue. Since this bIog is written in a typeface where l looks just like I, l think ℓ is a very good idea.
(PS: l swapped all the l’s for I’s in this repIy. Did you notice?)
That’s exactly why the SI recommendation is to use L when there is danger of confusion. This is similarly unambiguous and significantly easier to type.
Hi,
very interesting info.
You could maybe add some math about the price paid, more useful for common reader : like to boil my 500mL, it takes 0.xx $
By the way, that gives me more pleasure to install solar tubes in my garden.
Even that I have also losses (all kind of heat losses, no need to explain), the main source is free (except the price paid for the tubes and my time to install everything).
Regards,
Michel
Try a kettle like this one!
http://www.leevalley.com/en/garden/page.aspx?p=43901&cat=2,40733,40996,43901
Very cool! Also carbon-neutral if you burn wood. I want one (even though I wouldn’t go outside to make my morning coffee)!
In your measurements of boiling water on the stove top, in the microwave oven, and in an electric kettle, it appears that you might not have accounted for the heat of vaporization. This might help explain the dismal figures you were getting, because surely some portion of the water evaporated in the process.
On another chemical note, be sure that the vessel used in the microwave is clean and has nucleation sites on it. This theory is purely empirical.
I use a 1 quart pyrex measuring cup to heat my cold tap water for the hand ground coffee in the morning with a press pot**. The first day out of the dishwasher, the 20 ounces of water will visibly boil in 6 minutes or less in my microwave, pretty close to 6 minutes though. The next day it will take over 6 minutes. By the 4th day it could run for 8 minutes and still not bubble.
My theory is that “extra stuff” in my glorious Chicago water is depositing on the glass wall and removing the nucleation sites that would normally cause the bubbles to appear. The stuff is minerals of some kind and the dishwasher is able to remove them.
** You are suppose to grind your coffee fresh when you use it and I find the electric grinder too noisey before I have had my coffee. Yes, you can debate about mechanical energy from an animal (me) versus electric energy to grind the coffee.
Adding roughness (hard water scale) will increase nucleation sites. Very smooth materials have almost none. This is why you can super-heat water in a microwave and have it flash boil (dangerous). Eg: http://en.wikipedia.org/wiki/Superheating
If you’re purpose is to get the water heated to the boiling point, the heat of vaporization expended in evaporating some of the water is not useful and should be considered as waste inherent in the setup. Putting the lid on helps with this. A pressure cooker might eliminate more of this loss, as it would raise the boiling point and allow for less evaporation.
I did some experiments comparing oven/stove top cooking for my book and since then I have looked at savings from putting lids on saucepans for my blog. It is vital to take into account the energy from evaporating water and also the energy required to heat the pan. For example, in my basic boiling potatoes experiment with lid on, 19% of the energy went into evaporating the water and 15% went into heating pan and lid. If you take all that into account the gas hob itself works out about 30% efficient. The oven is much less so – baking potatoes took 6 times as much energy as boiling. I have recently posted on microwave cooking too: see http://energy-surprises.blogspot.co.uk/2012/05/do-microwave-ovens-save-energy.html
Thanks for the excellent additional information. Truly, I didn’t work hard to track down the loss channels, focusing rather on the end product: how much energy goes to the intended destination. Very useful to peek at the loss mechanisms, though. If you wanted to improve performance, that’s where you’d start.
Hi Tom,
You might find these few posts on the Aussie Homebrewer forums as a bit of an interesting read. The question was brought up here about boil times and brewing:
http://www.aussiehomebrewer.com/forum/index.php?showtopic=64381&st=0
and a link was posted inside in regards to insulation and lids etc and one of the guys set about doing some testing (albeit a bit dodgy) in here:
http://www.aussiehomebrewer.com/forum/index.php?showtopic=46683
Thought you might be interested in the amount of difference a lid makes. Also interesting is the ‘floatie’ idea, consisting of a cake tin or anything floating on the actual surface of the liquid.
A decent read and fairly entertaining too.
Cheers for your excellent blog,
Matt.
I brew beer at home every so often and have wondered about efficiencies in boiling water. I’d love to be able to have a solar water boiler to boil the 9+ gallons I typically use. But this brings up an interesting related point – that of the processes of preparing/brewing food/beer. Certain technologies (like boiling water with fossil fuel sources) have led to certain practices.
For example, there are two primary ways to “mash” a beer (basically the process of making a grain tea, called wort): infusion mashing and decoction mashing. Infusion mashing involves directly heating a kettle of water mixed with grain to certain temperatures (e.g. 120F for 30 minutes, 149F for an hour, then up to 175F to finish). This assumes you can precisely control the temperature of the burn point under the kettle, which is difficult with wood or solar heating. With a decoction mash, you heat exact measurements of water and wort to boiling point and add it to the main mash at certain intervals. This requires some up-front calculations of water-to-grain and boiling water-to-hot wort ratios, but it’s much simpler to do if you were to heat the water with a solar collector or other difficult-to-control heating source. I would imagine there are many other ways we heat water and food that make assumptions about the fuel source that could change to give us greater efficiency and flexible fuel options.
A related way in which brewers would efficiently brew is to use the same batch of grain to make multiple batches of wort. You can effectively rinse more wort out of the cooked grain to get a weaker beer after you’ve drawn out the primary batch of wort. This means you get one batch of strong beer and one or two more batches of successively weaker beer. Tradition holds that Belgian monks use to label their beers with 1, 2, or 3, each number designated one of those batches. 3 was the strongest and used for special occasions, while 1 was weakest for daily drinking.
Another cooking example: most days we make oatmeal in the morning by boiling 1.5c of water for .75c of rolled oats. I started trying out steel cut oats because I like the flavor. It turns out that with the steel cut oats, you can soak them overnight and then just warm it up in the morning. This is much more efficient than boiling a pot of oatmeal, but just requires some planning.
I am not particularly surprised about the inefficiency of a gas stove: I frequently go camping and I own an alcohol storm cooker (like a trangia, but mine is a cheap knockoff). That thing heats water about twice as fast as the open gas burners that you get for like 5$ to screw directly onto a gas bottle of about the same price (inkjet printers anyone?). And it does it on a miniscule amount of fuel, too.
Pity you couldn’t compare various kitchen stoves. Would be interesting to compare with induction, glass ceramic and iron cooktops. My guess is they’re all worse when accounting for generating and transmission efficiency at the plant, but induction might be close.
Boiling water is hardly anyone’s only need for cooking, but anyway very good article as usual. Makes one relativise.
What alternative ways of boiling water did you not mention ? What would be a game changer for food heating ? Any real-life solution systematicly close to 80% ?
A good start would be a mandatory efficiency-meter on each such device for end user to know…. Someday maybe… or not.
So when are you going to install a solar water heater in your home? They are incredibly efficient and could easily supply all your hot water needs in sunny San Diego.
One could measure electricity used per liter of solar hot water yielded, or measure the amount of sunlight needed to heat water X amount: so there are two efficiencies to measure.
There are solar hot water heaters for cold climates which use sunlight energy for pumping heat into the basement tank, f’instance: sunnovations has a coffee-percolator-like pump to get heat down to the basement. This pump uses the sun’s ‘boiling’ of a alcohol-water mixture; the bubbles drive the flow.
Please test an on-demand water heater, I’d be curious to see how it stacks up against the traditional.
I’m now very curious about how the under-sink electric hot water dispensers compare to regular electric kettles. On the one hand, they’re always on, so you lose something, though the unit doesn’t feel all that warm to the touch. On the other, they don’t have to heat as quickly. I’ve always classed it as absurd luxury, but maybe I’m just being efficient.
At two cups a day, 800 cups is a bit over a year’s worth of boiling. That’s a pretty short payback period for a home energy.investment.
A ΔT tip that applies especially to people in colder climates: after making your cuppa, refill the kettle (to its “minimum” line) straight away. The water will be warmed by residual heat from water remaining, and from residual heat in the kettle itself. When you make your next cuppa, the water will be starting from indoor ambient temperature or above, rather than outdoor or in-ground temperature.
(This applies even more if you live in an area with “aggressive” water – water that is capable of leaching the lead out of brass plumbing fittings. In areas with aggressive water, water supply authorities recommend flushing at least a cupful of water through taps before taking any water for internal use. In all areas they also strive to keep mains water below 12 °C to slow the growth of, uh, “biofilm” in the pipes.)
Great post. A few thoughts:
nutshell: you want the energy to go into the food, not anywhere else. When heating things in pots on the stove, cover the pot with a towel (be very careful of fire risk — this is probably more suited to an electric stove than gas). I find this means I can have water boiling on a setting of ‘2’ rather than ‘7’ (out of 9). Not precise, I know, but if that scale is linear, that makes a big difference.
Avoid using the oven where possible — shocking inefficiency. Use a dutch oven or similar, and cover it with a towel. We do cook pizza in the oven, but when we reheat it, we use a sandwich maker — works very nicely.
It’s also worth remembering that if you use Green Power, your electricity is not coming from fossil fuels, so a kettle makes better sense. 4 Months ago, we installed a solar hot water heater (Brisbane, Australia) — haven’t gone through the first winter yet, but I wouldn’t be surprised if we don’t need to boost more than a handfull of times each year…
Turning down the temperature of the hot water boiler, as you reminded yourself, might give room to all sorts of bacteria to start growing, like legionella. You need at least 50°C to effectively make the bacteria stop reproducing, and something like 55 to 60°C to kill it.
Having worked on related pathogens I think you are underestimating the power of chlorine. Legionella is a minimal risk and 50 °C is more than enough.
Growth occurs only up to app. 43-45°C. Hard to get infected by a pathogen if it cannot grow at 50 °C and the heater is continuously flooded with chlorinated water.
Legionella does not infect water heaters nearly as often as it infects cooling towers, which are a completely different system. No one drinks from cooling towers except in the rare instance that the plumbing is misconnected. The only major cases of the disease involved a cooling tower spray incident. Hence the name since the infected persons: http://en.wikipedia.org/wiki/Legionellosis
One other interesting fact. Canada decided to lower the minimum setting to 49 C from 60 C since many children and elderly were being burned by the prior minimum setting of 60 C.
http://canadasafetycouncil.org/home-safety/heated-debate-about-hot-water
So lowering the reservoir temperature to something like 40-45°C could be potentially dangerous, right? And nobody wants to shower with chlorinated water and smell like a swimming pool all day 😉
Not sure about such risks in heaters without a reservoir, I don’t think those will be susceptible to bacterial infections.
Infections are rare, indeed, just because temperatures in home boilers are high enough. And the reservoirs are ofcourse sealed, and the tap water is coming in clean… Still it happens from time to time in some isolated cases.
The classic office water cooler uses a heat pump to chill the water on the cold side, and heat the water on the hot side to something close to, but less that boiling. While I don’t think they are built for efficiency, this is the only example of a heat pump water heater that I encounter on a regular basis (and of course it is electrically powered, but the problem of getting energy from fossil fuels will correct itself before you know it).
Such a heat pump is probably the most efficient existing way to make coffee or tea.
Another great post!
A note to your readers – there are heat-pump hot water heaters available. A good option if you’re replacing a traditional electric hot water heater. I have one of these and it has saved me about 300kwh/month since installed. I haven’t ‘done the math’ myself (shame on me! 😉 ), but I think these are more efficient that on-demand point-of-use electric hot water heaters.
Also, if you’re replacing a central air system with a heat-pump system, ask if the manufacturer has a hot water option – these should be even more efficient than a stand alone heat pump hot water heater.
Excellent work. I had no idea efficiencies were that low.
I bet the efficiency of an electric hot water heating tanks would be pretty good. The element is immersed in the water. The surface to volume ratio is small compared to an electric kettle, so those losses would be less. It doesn’t boil and evaporate water.
Heat pumps seem attractive with a coefficient of performance of 3,1 kWh(e) input of 3 kWh(t) output. But if the electricity is generated with fossil fuel with typical efficiency of 33% [3 kWh(t) for 1 kWh(e)] you might just as well have burned the fossil fuel at home.
Hello Tom,
You may be a data fanatic, but you don’t seem to know much about water heaters. So here’s a little more information for you.
First of all, there is more than one type of gas water heater. The less expensive versions, commonly purchased by landlords who don’t pay the gas bill, tend to use so called atmospheric burners, much like the ones on a typical gas stove top. These typically have burner efficiencies in the range of 60 to 65%, which you have confirmed by your testing.
The better and more slightly more expensive gas water heaters typically use so called power burners, where a small blower is used to achieve better mixing of the gas and air mixture, and can therefore use less excess air in the mixture. These more efficient water heaters will typically deliver around 80% efficiency, and reduce fuel use by 20 to 25% (since we stared from 65%, not 100%).
Second, most new gas water heaters now use an electronic ignition system, thus eliminating the standing gas pilot.
Third, you can often reduce the standby heat losses from tank type water heaters by making sure you have a thermal break in the piping at both the inlet and outlet of the tank. These short pipe nipples with the thermal break cost about $1 more than the plain pipe nipples without the thermal break, at big box stores like Home Depot, but the plain nipples can cost you $100 or more per year in higher standby heat losses.
If your existing water heater piping does not have these thermal breaks, you may be able to install a foot or so of PEXX tubing in place of copper tubing to minimize these standby losses. You may be able to do this as a simple DIY project using push on fittings such as the “Shark Bite” fittings available at Home Depot, if you local building codes allow this.
And last but not least, there are simple timers that can be used to turn off the water heater for long periods overnight, and maybe during the day if nobody is at home. Fuel savings from a six to eight hour overnight shutdown can be around 10%, and using both day and night shutdowns can often yield 15 to 20% fuel savings.
The combined effects for these simple changes can often reduce energy use for water heating by up to 50%. And this is often possible with your existing water heater, without spending $1500 or more for a new tankless water heater. So how about checking out these issues and reporting back to us in a few weeks?
Thanks for the useful info. You’ve been thorough enough that there is no need for me to “report back.”
Hello Tom,
With your big audience, I think it would be helpful if you tried some of these suggestions, and then reported back on the results. I have found over the years that most homeowners respond much better to real world examples with reported savings, than they do to theoretical explanations. Think of your blog as the modern version of Teddy Roosevelt’s “Bully Pulpit”.
Maybe some of your neighbors have a newer gas water heater with a power burner and no standing pilot. You could set up your metering system at their house and compare the energy use to the amount of water used. And if the savings are significant, you could calculate the simple payback from replacing an old water heater with a more efficient one, before the old one fails. These savings can be very cost effective, and if multiplied by thousands of homes, the total savings could be significant.
If you find that your water heater does not have the thermal breaks in the inlet and outlet pipes, you can probably fix that yourself using the PEXX tubing method, especially if you have more free time during the summer months. This problem and fix applies equally well to electric water heaters. When I did this fix on the electric water heater where I live, it saved me $15 each month on my electric bill. It’s been three years now, so I’m up to about $540 in savings from about six hours of work, including the trip to Home Depot.
You forgot to mention heaters with exhaust gas condensers 😉
http://en.wikipedia.org/wiki/Condensing_boiler
I like this. I have used an electric kettle for hot water, assuming it was more efficient than the cooktop. My expectation is that the energy transfer in the microwave would not be that efficient because there are multiple conversions. (I believe that the device that generates microwaves is a magnetron instead of a klystron – picky, picky).
I wonder how a water heater insulation kit would affect energy use.
Since water heatng and home environment conditioning are two of the largest users of energy in the home, I was thinking about monitoring energy use as a function of degree days so that it was possible to quantify the effect of improvements to my home.
Thank you for the interesting information (and thanks to the commenter who suggested thermal break fittings). Did you, perchance, calculate your actual cost for the different methods? I’m curious if the amount you pay to heat those vessels in those different manners equals out (not that end-user cost should justify wasteful practices, although it often does.)
To make a cup of tea cost me .03Kwh to make a little over one cup of tea useing a Sunbeam AquaW electric kettle. All our electricty is Hyrdo. The kettle itself maxed out @ 1400Watts. Since I was curious, I made 2 slices of toast, The toaster consumption ~1050Watts.
Total for ~1.5 cups worth of water and 2 slices of toast .09Kwh
I have boiled water on our electric stove, full blast no lid exactly as you did here, but its a little tougher as I dont have a 3-phase Kill-o-Watt to measure it with. 🙂 That would have been an interesting comparision. However, consulting with the elder(my Mom) informed me, she cant stand boiling water that way as it makes her pots all ‘scaley’. So even if it were highly efficent to boil water in an open pot, she wouldnt allow it anyhow 🙂
One small pedantic note; the RF oscillator in a microwave oven is a magnetron,
not a klystron.
Here’s my dilemma about kettles and such.
Should I fill my kettle with cold tap water, or hot? I have a basic gas hot water tank with about ~4m of very poorly insulated copper pipe between it and the sink. My stove is a 2yr old electric. I assume the hot water in the pipe has cooled prior to withdrawl, but post-kettle-filling it will be full of hot water.
I live in ontario, we’re almost all nuclear/hydroelectric generation.
Hello Andrew,
If your hot water piping is copper tubing with soldered fittings, it is best to never drink any of the hot water coming out of the tap. Start with cold tap water after flushing the pipes for a few seconds, and then heat it in your kettle. Very little difference in cost, and much safer.
Another great post.
However, your gas oven calculation may be off. If it has a electric heating element to light the gas, it probably stays on the whole time the gas is on. I believe that this is done for safety. I remember reading years ago that the element could be 350 W or more. It probably needs to be checked with a Kill-a-Watt.
My TED system would tell me; as it is, the oven being on seems to draw no appreciable electric power.
Tom,
While the 1st law efficiency (e1) of your water heater is 64%, the 2nd law (or exergy*) efficiency (e2) is actually much less.
Here’s a qualitative description from physicist Robert Ayres on this very subject:
“The correct way to measure efficiency is to treat both the input and output in exergy terms. The input (say natural gas) has a high exergy content because it burns at a high temperature, whereas the output (hot water) has a very low exergy content because it is only a little above room temperature (as compared to the flame heat). So, the real exergy efficiency of a hot water heater must be very low, in the sense that the same amount of heat produced by the flame could have done a lot more work than it actually ends up doing when you wash dishes or take a shower. In effect, the heater wastes most of the temperature difference between the gas flame and the water. In exergy terms, the efficiency of most water and space-heating systems was (and still is) only around 5 percent.”
Page S4 of the supporting information from this paper gives a simple e1 and e2 calculation for an electric water heater. The results show how a process can have a high e1 while simultaneously having a low e2.
While a 2nd law analysis doesn’t directly address the economics of the process in question, it can help us match energy quality with process need, i.e., not using finite, high-quality fuels to heat a room to 75 deg F. Given that exergy is consumed (unlike energy), I think it’s important to not only trace where the BTU’s go (e1), but how their quality is degraded (e2) so that we can efficiently manage our exergy stocks (fossil fuels) and flows (solar radiation).
(For those who’re interested in seeing some more quantitative examples, the 5th edition of Cengel’s and Boles’s thermo text devotes an entire chapter to exergy and second law efficiencies.)
*Exergy can be defined as the maximum amount of work that can be extracted from a system as it reversibly approaches equilibrium with its environment.
Great comment. I think what you’re saying is: “use energy-dense sources (eg. fossil fuels, electricity) where they are needed only, for example electronics systems. Use energy sparse sources (eg. solar) elsewhere”
This is another good argument for using solar heating, both for one’s house and one’s water, and is why having a solar hot water system is so much better than having solar PV and using it to power an electric water heater.
Nice post! I was wondering if you could test magnetic Induction heating efficiency?
In northern climates the waste heat from a water heater placed in the bathroom increases the value of the energy used and also the cooking loss is captured in part by heating the home.
What about using a heat exchanger pan such as http://www.ultralightoutdoorgear.co.uk/primus_etapower_pots_with_heat_exchangers.html
I’d be curious to know if single-cup water-heating appliances are any more efficient (especially than electric kettles, where it avoids the “too much water heated” problem). The one I’m familiar with is the Sunbeam Hotshot. You fill your cup at the tap and dump just that much water into the top of the hotshot, which rapidly heats that water and then dispenses it, for tea or instant soup or whatever. They were very popular in college because they heated one cup very quickly, and were pretty low energy because we could use them in the dorm (where microwaves and hairdryers shorted out the electrical all the time). I see from a quick google that they’re considerably updated (heat up to 16 oz. — mine only did 12, I believe; and much nicer design), but maybe that also includes energy efficiency.
(And yeah, as someone in a four-season climate, we definitely use the oven strategically, heating it up for long-cooking items in the winter, when the heat will kick on less often when I’ve got the oven on, and trying not to use it much in the summer because it makes the kitchen SO. HOT. The cooktop doesn’t heat the room nearly as much, but you more often have to stand right over it and attend to it, so I’m less-willing to do that in the summer.)
Excellent post! I’m mildly obsessed with energy efficiency, but haven’t the expertise (or drive I suppose) to run the numbers like you’ve done. So thanks. I also have another challenge for you, should you choose to accept it: slow cookers. I like to make my own hummus (highly recommended) and prefer to use dried beans. I soak ’em overnight but they still take hours to cook — maybe 4 hours on my cooker’s “high” setting and close to 8 on “low”. Of course you do them on the stove too at very low heat, which is similar to the low setting. I found a site on the ‘Net that had done some experiments and concluded that the burner would actually be more efficient given the long cooking time. But your analysis would surely be more accurate.
Anyway, thanks again for the article, and if you do decide to test a slow cooker please e-mail me when you post the results!
Great article!
I like your experimental spirit. I have been pursuing some of the same data goals you talk about here, and a=have a few suggestions.
First off, I sub-metered my water heater to isolate its use (I’ve got tenants and can’t turn off their heater, nor control their hot water use). But I also have a flow meter on my water heater (inlet side), and numerous temperature sensors. And my water heater efficiency calcs are just the opposite of yours; namely, much too high. I’m finding efficiencies of 75-80%. Why, that’s the efficiency of the burner itself! Can’t be right, what with stand-by and other losses. I’m still puzzling that one out (and will end up buying an accurate gas meter with a pulser, rather than the $50 eBay special I now read manually).
Your numbers for the stove top surprise me. I’ve got a copy of a report done by Lawrence Berkeley National Labs in 1998 or so on cooking appliances that claims about 40% efficiency for gas cook tops, and twice that for electric stoves (assuming flat cookware). Their numbers for ovens are 7% for gas and 14% for electric (no flue vent for electric), self-cleaning (more insulation; non-self cleaning were 1 point lower). And microwave ovens were around 50%. I haven’t tried these myself; I am looking at sub-metering my gas range (my wife is planning a major kitchen remodel — that’s my chance!)
And your observation that most people put more than enough water in the kettle is spot-on. Of course, that’s true for any kind of kettle with any fuel source.
Here’s a suggestion to increase the efficiency (whatever it is) of your gas range: the TurboPot ( http://theturbopot.com/ ). Actually, a series of aluminum cookware with heavy grooves in the bottom to increase the surface area and capture more heat from a gas flame. I bought the tea kettle, and figure the grooves increase the surface area of the bottom by a factor of about 4.4. I monitored temperature vs. time with both the TurboPot kettle and our other kettle on a couple of different burners. The numbers were 5 and 9 (the ratio of the degree per minute slopes); so the TurboPot boiled in 5/9 the time of the other one. And yes, the TurboPot did much better on the larger burner than the smaller kettle (the other kettle was too small for that burner).
Anyway, thanks again for your stimulating article. I’ll try to recreate your experiments as time and equipment allows.
After seeing your remarkable experiments and your results, i tried to reproduce one of them this morning during my breakfast. I boiled some water in a pan on a gas burner. As i am used, i put a lid and used the smallest burner in order to reduce the flame surface.
Here are the data. All my units are in SI or close (i am living in a country where metric units were first applied. So all data are directly in these units. I have a hard time when reading data from USA). Sorry i use comma for decimal separation; this would be my French touch. Sorry also for my bad writings.
550 g of water +/- 4g
390 g of pan without the lid. It is out of aluminum.
Fortunately i have the gas-meter just above the burners, which makes much easier the measurements. The reading is assumed in standard m3.
Water was about 20°C at start. I did not use a thermometer in the water but looked at the gas meter when it started boiling. Pressure at my flat was 1009 mbar, so boiling temperature is at boiling point, 100,0 °C.
So temperature difference is 80 +/- 1 °C.
From the start to boiling point, 10,5 +/- 0,2 in dm3 of gas.
The main uncertainty comes from the conversion from the volume of gas to heat power. This coefficient is not constant as it depends on the gas mixture. In turn this mixture depends on the gas origin, Norway, Russia, Algeria, North sea… (unfortunately our main gas field Lacq in basin d’Aquitaine is near exhaustion after delivering more than 90% of its resource, about 9,0 T.f3).
I looked at my last gas bill to know it : 10,97 kWh(HHV)/m3(gasmeter), or 39,5 MJ(HHV)/m3(gasmeter)
For the water with 4,18 J/g/°C i got 184 kJ(th) +/- 5 (to be large).
To be compared with my gas consumption or 415 kJ(HHV)
So i got 44 % (th/HHV)
or nearly 49 % (th/LHV)
For natural gas approximated to methane, 1,0 J of LHV = 1,1 J of HHV. It is the first loss to notice, unavoidable for this sort of application.
So i am better than you. Not sure why.
Al pan : Cp = 0,90 J/g/°C (lower than water as a water molecule has more degrees of vibration than the Al atom and has lighter molecular weight, 18 against 29 g/mol). So 122 kJ of heat for the pan if all at 100 °C. Of course not the case. But some heat flows toward the air around the pan, mostly by conduction across the pan and convection.
I will try again to see if reproducible.
Yours sincerely
XC
Yes, please stop using the crazy US-only units.
Frankly, anybody who is interested enough and numerate enough to read your blog (and comments) is numerate enough to either natively use or be able to convert to SI. (I’ve lived here 25 years and I still don’t know what a degree Fahrenheit is, except for – 32 * 5 / 9)
BTUs and cubic feet and foot-pounds can only ever lead to error, and never deliver practical enlightenment.
It is unfortunate, to be sure, that the U.S. has stuck to the old units. Drives me crazy as a scientist. But I must write for two audiences.
You point out that anyone numerate enough to enjoy Do the Math should have no trouble converting units, yet after living in the U.S. for 25 years, you lack intuition for Fahrenheit. I think this illustrates that we get stuck with certain intuitions. The U.S. audience needs to see things in more familiar terms (like what shows up on their meters, their bills, at the gas pump, etc.—daily life envelops us in a unit system).
I try to offer both in most cases, with a slight leaning toward the metric—though it may not seem so if the imperial units chafe.
Like most of America, I’m stuck. But having both unit systems present may help American readers develop intuition and familiarity with metric measures in some very small part.
I’ve travelled in South America where “electric showers” are used because there is no heat loss from storing hot water. A 240 volt line goes to the shower head. When the water flows the current turns on and heats the waster as it goes by. I saw lots of char marks in showers, though. Don’t reach up to wash your armpits.
I own a all electric house and I did my own non-scientific experiment years ago. The results led me to buy a toaster oven for anything smaller like pizza that I would have cooked in my oven. It’s nice to see someone add real numbers to what I already discovered to be true.
Thanks for taking the time for experimentation and the interesting useful results.
Here/s a question maybe only physics and chemistry collaborators can investigate:
I’ve often notice my stove flame has occasional bursts of yellow among the blue flame. There are no adjustment issues as it can often burn purely blue. I have thought it might be excess moisture delivered in the gas supply or even “contaminate” mixing as I observed a new supply connection being made during a brother’s house renovation (they attach a saddle to the distribution pipe and under full pressure, punch a new supply line hole that leaves the remnants in the big pipe).
But then I read about fracking and apparently the gas has to go through a purification process to separate out CO2. So now the question becomes are those orange bursts due to a adulterated form of gas that would of course muddy up your measurements. Please have a look at your flame during different times of the day, maybe you might see what I have often observed. It would be great to know the purity of the gas delivered.
john
This is a timely post as I am currently in East Timor delivering a training program for installing small PV systems in remote communities. One of the other programs is the rollout of locally manufactured efficient wood stoves to replace inefficient.three-stone fires.
A few days ago, some of my colleages were commenting about how we were improving on the very basic technology and bringing it closer to our (western) technology. I pointed out that, in some ways, we were actually delivering superior technology since we were still using a basic “3-stone” system but we had replaced the stones with a metal grate or hob and the wood with gas.
The efficiency of the wood stoves in ideal conditions can be as high as 40% but is often much lower, around 25%-30%. Seems we also have some to way to go.
You may be interested in David MacKay’s take on this from back in 2008 at http://withouthotair.blogspot.co.uk/2008/10/how-to-boil-water.html
PS Congratulations on a great blog!
What model slide rule is in your title image, just curious 🙂
K & E N4081-5 Log Log Duplex Decitrig (1947). 22 inches (41 cm), and can carry three digits all day long…
Hello, from what you say it looks like you have found a method to extract, process and transfer natural gas at 100% efficiency. Since I don’t think this is the case, you should correct your results to reflect the fact that there are losses in the gas distribution chain too, to equilibrate the unfair handicap you gave to the electric source. Unfortunately this is a prejudice I encounter every day working on the electric cars business. You should define better the context of your experiment, and decide how “deep” you want to go with the analysis and apply the same measurement method to all your experiments.
Hey,
very interesting blog post. If you’re interested in energy monitoring you should check out our open energy monitor project: http://openenergymonitor.org/
Using a microwave is even worse if you don’t turn it off at the wall when it is not in use unless it is one with a clockwork timer on/off switch.
If you have a microwave with soft bush button controls and/or a digital display then the microwave will use more energy “waiting” for you to use it than it uses when it is actually “in use”.
Good point. As an approximate rule of thumb (perfect if microwave is 1440 W), each minute of microwave use in a day is matched by each Watt of idle power. I have seen soft-button idle powers range from 1 W (more energy into cooking than idling) to 4 W (closer to 50/50 under typical use). So I would modify your “will use more energy” to “might use more energy.”
Hi Tom,
Very interesting post. I have wondered about many of these issues myself, and some I hadn’t ever thought of (microwaves are that bad, huh?)
I was hoping your water heating article would cover getting the water to your house, since you usually do the big picture thing. Have you considered, living in southern California, how much electricity is embodied in the 500mL of water? I bet it’s not much, but still higher than, say, Portland or Seattle…
I’ve heard that 10% of all the kWh used in CA are for moving water, and a further 9% are for treating it and waste water. The opinion of “this can’t go on!” is just as valid with the American West’s water system as it is with the world’s energy system, and might come to a head even sooner than oil, energy, or exponential growth.
Thanks,
Val
Couldn’t resist. California’s annual electricity generation is 206 billion kWh, 8% of which goes to pumping water.
The per-capita water use (quick search; may be off) is 1000 gallons/day (4000 liters/day). Makes some sense to me, based on some knowledge of residential use and that agriculture takes more. Multiply by 37 million people, and 365 days for total gallons.
So I get 0.001 kWh put into each gallon. 1 Wh is 3600 J, which would lift a gallon (4 kg) 90 meters. Seems plausible.
By comparison, boiling that same gallon of water would take about 400 times as much energy.
Makes sense. Our water moving system is mostly benefiting ag… it is probably true that san Diego is some multiple higher than average, since it is further away from the source even than LA. Plus there are chemicals produced with oil or electricity to treat the eater that might add another factor of 5 to the rrsidential water energy burden. This starts getting significant in domestic energy, where you boil maybe 1/1000th of the water you use to water the lawn or garden. Not that you personally use water for that,but san diegans at large. Not to mention LAers, bay areans etc.